CF939F Cutlet题解

前置

单调队列（没学过或忘了点这里）

简化题意

有一块牛排，要求对它烹饪 \(2n\) 秒，可在给定的 \(k\) 个时间段中将它翻转任意次，使得牛排两面都受到了 \(n\) 秒的烹饪。

状态设计

• 可以发现当总共煮了 \(i\) 秒，其中一面如果煮了 \(j\) 秒，自然可以求出另一面为 \(i-j\) 秒，所以我们可以设状态为 前 \(i\) 秒没在烤的面煮了 \(j\) 秒的最小翻转次数，但由于时间 \(n\) 最大为 \(10^5\) ，所以这个状态必然是 开不下 的。

• 不过，可以发现题目要求必须在 给定的 \(k\) 个区间内才能翻转 ，所以可以以每个区间作为一个状态。设 \(dp_{i,j}\) 表示第 \(i\) 个区间结束时，没烤的面煮了 \(j\) 秒的最小翻转次数。最终答案为 \(dp_{k,n}\) 。

转移

考虑有哪些情况会构成转移：

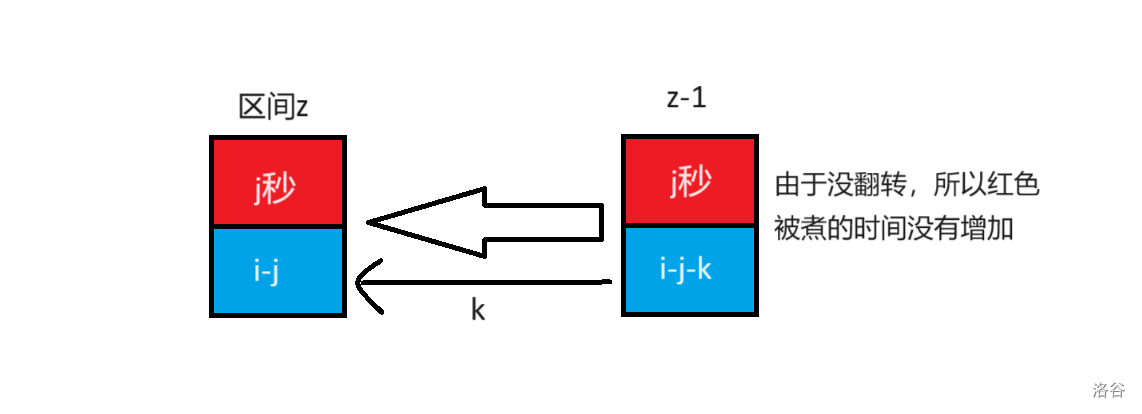
• 一种情况是不翻转，这时没煮的面煮的 时间没有增加 ，所以直接继承上一个区间的状态。

  则转移方程为 \(dp_{z,j}=dp_{z-1,j}\) 。

• 考虑在一个区间内翻转多次（钦定每次翻转都在 \(z-1\) 区间结束后）：

  • 如图所示，翻转很多次可以转换为翻转 一次 或翻转 两次 的情况。（附：每个区间 \(z-1\) 到下一个区间 \(z\) 都看作在区间 \(z-1\) 结束时 立刻翻转 ）

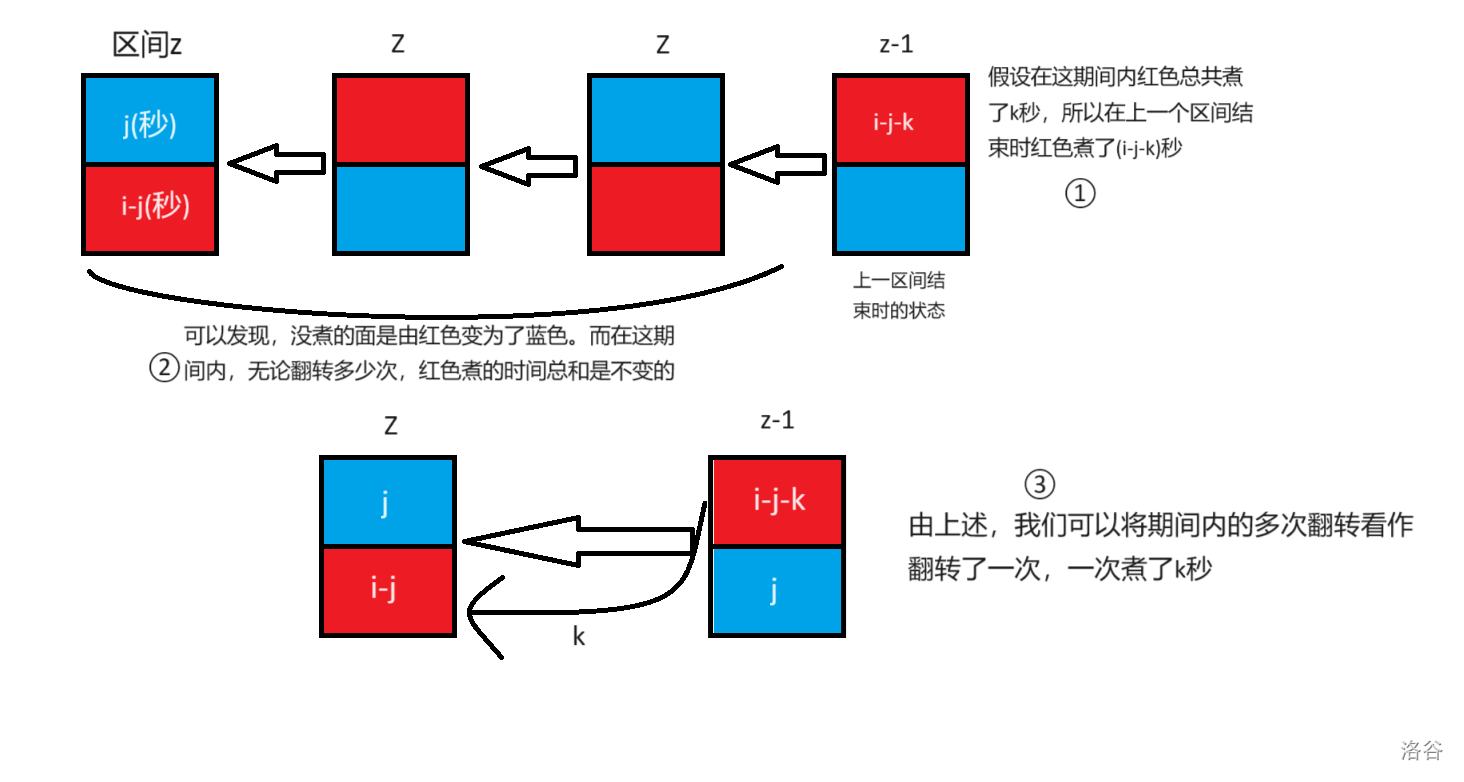
    • 翻转 一次 ：

    1. 由图，可以得出转移 \(dp_{z,j} = \min ( dp_{z-1,i-j-k} ) +1\) 。

    2. 因为只能在区间 \(r_z\) 至 \(l_z\) 之内翻转，且结束时间为 \(r_{z}\) ，所以 $( r_{z}-k \ge l_{z} ) \to ( 0\le k\le r_{z}-l_{z}) $ ，并且满足 \(( r_{z} - j - k \ge l_{z} )\) 。

    3. 至于 \(j\) ，我们可以发现蓝色的枚举范围 $( 0 \le j \le r_{z} ) $ ，但如果再算上 \(k\) ，且两者都取最大值，那么 \(i-j-k\) 很可能会得到负数，造成越界，所以想用 暴力 拿部分分也是较为 困难 的。

    4. 因为所设状态为 区间结束时间 ，所以 \(i\) 无需枚举，为 \(r_z\) ，方程则变为 $ dp_{z,j} = \min \limits_{ 0 \le k \le r_{z} - l_{z} } ( dp_{ z-1,r_{z}-j-k } )+1$ 。

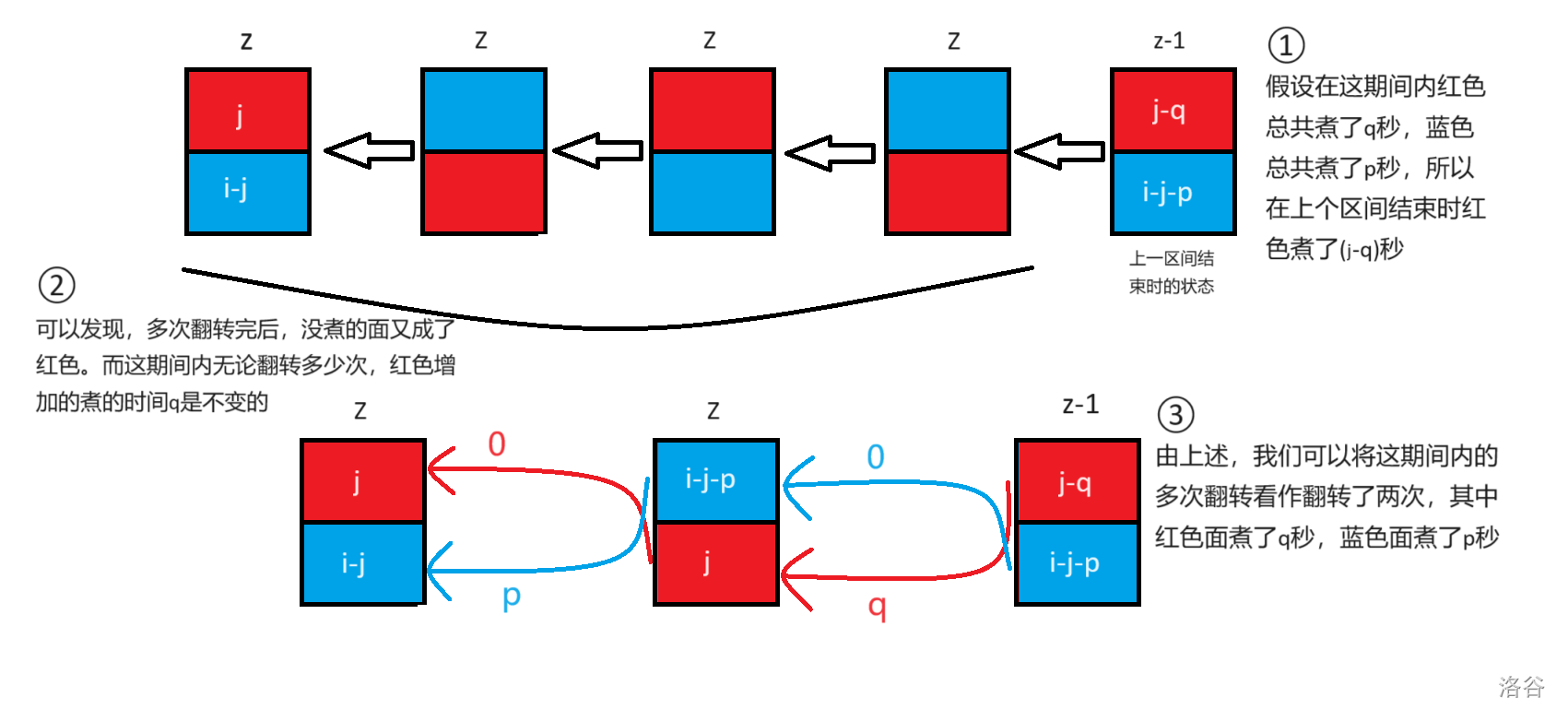
    • 翻转 两次 ：
    1. 由图，可以得出转移 $ dp_{z,j} = \min ( dp_{z-1,j-q} )+2 $ ，同上 \(({ 0 \le q \le r_{z} - l_{z} })\) ，且满足 \(( l_{z} \le j-q \le r_{z} )\) 。

  则所有 转移方程 如下(为了方便这里 \(i\) 为第 \(i\) 个区间)：

  \[dp_{i,j}=\begin{cases}dp_{i-1,j}&{0\le j\le r_{i}}\\
  \min(dp_{i-1,r_{i}-j-k})+1&{0\le k\le r_{i}-l_{i}}\\
  \min{(dp_{i-1,j-q})+2}&{0\le q\le r_{i}-l_{i}}\end{cases}
  \]

优化

• 在分析翻转 一次 的方程时，我们发现用暴力跑 \(dp\) 是会越界的，且 \(( 0 \le n \le 10^5 )\) ,且枚举 \(j\) 与 \(k\) 也会 \(TLE\) 。那么，怎么办呢？
• 根据翻转 一次 和 两次 的方程中，我们可以发现，每当枚举到一个新的值，都会和原来的值取更小值，最终会取得这一区间内的最小值。每次更新，都会更新更小值，这是符合 单调性 的，所以可以使用 单调队列 进行优化。
• 由于变成在一个范围内取最小值，所以 \(k\) 和 \(q\) 取 最大范围 \(r_{i}-l_{i}\) 。
• 具体的，我们可以将翻转 一次 的方程看作在 $ dp_{ i-1,r_{i}-j-k } $ 到 \(dp_{ i-1,r_{i} }\) 之间取最小值，将翻转 两次 的方程看作在 $ dp_{i-1,j-q} $ 到 $ dp_{i-1,j} $ 之间取最小值(这里 $ r_{i}-j-k $ 化简后为 $ l_{i}-j $ ，它作为 出队条件 ，所以不用担心越界)。
• 则最终方程如下：

\[dp_{i,j} = \begin {cases} dp_{i-1,j} & { 0 \le j \le r_{i} } \\
\min ( dp_{i-1,r_{i}-j-k})+1 \to \min (dp_{ i-1,r_{i}-j-(r_{i}-l_{i}) })+1 \to \min (dp_{ i-1,l_{i}-j })+1&{ 0 \le j \le r_{i} } \\
\min ( dp_{i-1,j-q} )+2 \to \min (dp_{ i-1,j-(r_{i}-l_{i}) })+2 \to \min (dp_{ i-1,j-r_{i}+l_{i} })+2&{ 0 \le j \le r_{i} } \end {cases}
\]

到了这，这题就解完了，欢迎指出题解中错误，如需代码也可以私我。