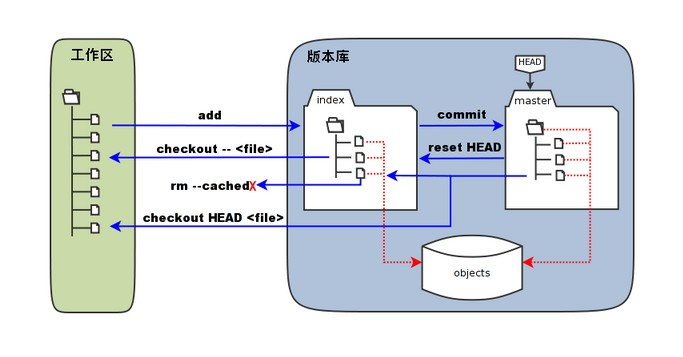
Git入门--九五小庞
Git入门--九五小庞的更多相关文章
- WinMTR 网络测试工具-九五小庞
WinMTR(建议优先使用) 百度下载工具 链接:https://pan.baidu.com/s/19ArKSTA2amsa4p6vHegDIQ 提取码:cy4y WinMTR是mtr工具在Windo ...
- Oracle 11G R2安装说明 -九五小庞
教程版本Oracle 11.2.0.1.0
- VMware安装Centos7 -九五小庞
VMware安装Centos7超详细过程(图文) https://blog.csdn.net/babyxue/article/details/80970526 安装centos7的时候 启动会提示Pl ...
- 什么是Nginx -九五小庞
- Oracle错误 ora-12514 解决方法-九五小庞
成功连到数据库上之后,查看listener状态:lsnrctl status status READY 状态,需要由非归档转为归档模式,故操作如下: 1.关闭数据库shutdown immediate ...
- oracle创建/删除 用户,表空间-九五小庞
以下红色标示的都是可以修改的字段 可以按照如下顺序来创建表空间,创建用户,以及删除表空间,删除用户 查看oracle数据库已有的表空间路径 select name from v$datafile; 1 ...
- ORA-01033错误解决方案-九五小庞
Microsoft Windows [版本 6.3.9600](c) 2013 Microsoft Corporation.保留所有权利. C:\Users\Administrator>sqlp ...
- oracle数据库备份 -九五小庞
oracle数据库备份
- oracle数据库创建数据库实例-九五小庞
oracle数据库创建数据库实例
- Oracle两个数据库互相访问-九五小庞
Oracle两个数据库互相访问
随机推荐
- 使用了下UOS浏览器,突然不想说话了
使用了UOS20,安装上了,但是要激活:我蒙了!好吧,适用下吧: 看下浏览器情况: UOS浏览器 5.1.2365.0 (正式版本) stable (64 位) 修订版本 3cfecd947e7bc5 ...
- 操作系统综合题之“采用时间片轮转调度算法(Round-Robin,RR)执行,分时系统中的进程可能出现的状态变化”
一.问题:某分时系统中的进程可能出现下图所示的状态变化,请回答下列问题: 1.根据图示,您认为该系统采用的是什么进程调度策略? 2.把图中所示的每一个状态变化的原因填在下表相应位置. 变化 原因 1 ...
- 网络编程:反应堆reactor框架设计
https://app.yinxiang.com/fx/7e601cad-6501-4fe7-8e4e-f0fbd9d02c4b TCP 高性能网络框架需要满足的需求有以下三点: 1)采用 react ...
- Python标准库学习之logging
前言 在python程序中,出于调试监测或者追踪(track)的目的,一般会在关键的部位加print语句来输出监测的变量值,但对于复杂的程序来讲,这样的调试手段就远远不够了,这也是logging库存在 ...
- codeup之冒泡排序
Description 从键盘上输入10个整数,用冒泡法对这10个数进行排序(由小到大). Input 以空格分隔的10个整数 Output 依次输出排好序的10个整数,每个数占一行. Sample ...
- 在LLVM中的greedy Register Allocation pass代码详解
LLVM 贪婪寄存器分配器(RAGreedy)详细处理流程 日期: 2025年5月29日 摘要 本文深入分析 LLVM 贪婪寄存器分配器(RAGreedy)的处理流程,详细描述从优先级队列获取虚拟寄存 ...
- mysql 添加外键约束
添加外键 alter table table_name add foreign key fk_product_id (product_id) references product(id) tabl ...
- Java 17 java.util.HashSet 类源码分析
在绍了 Map 集合的一种典型实现 HashMap之后 ,我们知道,自Java 8起HashMap 是由数组+但链表+红黑树构成,相对于早期版本的 HashMap 实现,新增了红黑树作为底层数据结构, ...
- 【pr】利用lrc快速导入歌曲的歌词
确保你的bgm是原汁原味的,没有经过变速或剪辑 下载lrc https://www.musicenc.com/ pr不能直接导入lrc,需要将lrc转换成srt https://www.lrccon. ...
- 「Note」图论方向 - 图论进阶
1. 2-SAT 1.1. 介绍 对于一些节点,每个节点存在两个状态(非 \(0\) 即 \(1\)),我们给出一些如下类型的限制条件: 节点 \(i\) 状态为 \(1/0\). 若节点 \(i\) ...
