最短路径——Bellman-Ford算法

一、相关定义

最短路径：求源点到某特定点的最短距离

特点：Bellman-Ford算法主要是针对有负权值的图，来判断该图中是否有负权回路或者存在最短路径的点

局限性：算法效率不高，不如SPFA算法

时间复杂度：O（mn）

【具体与dijkstra算法的比较】

Bellman-Ford算法为何需要循环n-1次来求解最短路径？Dijkstra从源点开始，更新dis[]，找到最小值，再更新dis[]……每次循环都可以确定一个点的最短路。Bellman-Ford算法同样也是这样，它的每次循环也可以确定一个点的最短路，只不过代价很大，因为 Bellman-Ford每次循环都是操作所有边。既然代价这么大，相比Dijkstra 算法，Bellman-Ford算法还有啥用？因为后者可以检测负权回路啊。Bellman-Ford 算法的时间复杂度为 O(nm)，其中 n 为顶点数，m 为边数。

【负权回路】

开始不懂，看了下面的图和我的算法描述后就懂了：

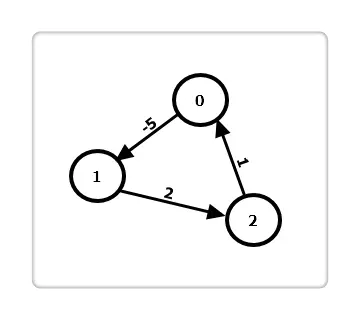
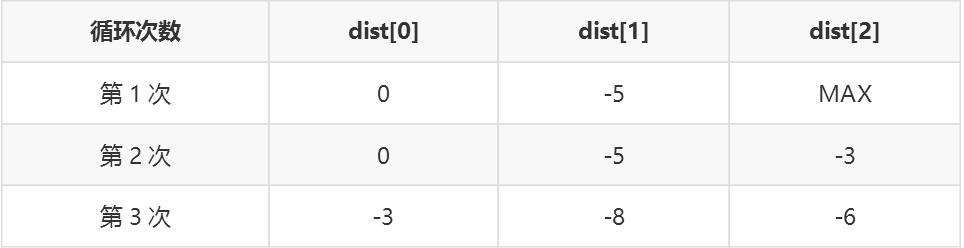
在循环n-1次的基础上再次遍历各边，对于所有边，只要存在一条边e(u, v)使得 dis[u] + w(u,v) < dis[v]，则该图存在负权回路。

【松弛操作】

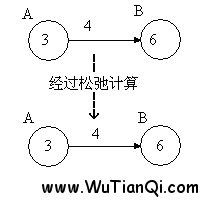
如左图所示，松弛计算之前，点B的值是8，但是点A的值加上边上的权重2，得到5，比点B的值（8）小，所以，点B的值减小为5。这个过程的意义是，找到了一条通向B点更短的路线，且该路线是先经过点A，然后通过权重为2的边，到达点B。
当然，如果出现右边这种情况，则不会修改点B的值，因为3＋4>6。

二、算法描述

关键词：初始化    松弛操作

主要变量如下：

int n　　　   表示有n个点，从1~n标号

int s,t 　　　s为源点，t为终点

int dis[N]　  dis[i]表示源点s到点i的最短路径

int pre[N]　 记录路径，pre[i]表示i的前驱结点

bool vis[N]  vis[i]=true表示点i被标记

【初始化】

dis数组全部赋值为INF，pre数组全部赋值为-1（表示还不知道前驱），

dis[s] = 0 表示源点不要求最短路径（或者最短路径就是0）。

【松弛操作】

对于每一条边e(u, v)，如果dis[u] + w(u, v) < dis[v]，则另dis[v] = dis[u]+w(u, v)。w(u, v)为边e(u,v)的权值

注：上述循环执行至多n-1次。若上述操作没有对Distant进行更新，说明最短路径已经查找完毕或者部分点不可达，跳出循环；否则执行下次循环。

【检测负权回路】

为了检测图中是否存在负环路，即权值之和小于0的环路。

检测的方法很简单，只需在求解最短路径的 n-1 次循环基础上，再进行第 n 次循环：对于每一条边e(u, v)，如果存在边使得dis[u] + w(u, v) < dis[v]，则图中存在负环路，即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。

【小结】

Bellman－Ford算法可以大致分为三个部分：

1. 初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。
2. 进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。
3. 遍历途中所有的边（edge（u，v）），判断是否存在这样情况： d（v） > d (u) + w(u,v)，若存在，则返回false，表示图中存在从源点可达的权为负的回路。

之所以需要第三步的原因，是因为，如果存在从源点可达的权为负的回路，则将因为无法收敛而导致不能求出最短路径。

三、代码实现

#include<iostream>
#include<stack>
using namespace std;

#define MAX 10000  //假设权值最大不超过10000

struct Edge
{
    int u;
    int v;
    int w;
};

Edge edge[10000];  //记录所有边
int dist[100];     //源点到顶点i的最短距离
int path[100];     //记录最短路的路径
int vertex_num;    //顶点数
int edge_num;      //边数
int source;        //源点  

bool BellmanFord()
{
    //初始化
    for (int i = 0; i < vertex_num; i++)
        dist[i] = (i == source) ? 0 : MAX;

    //n-1次循环求最短路径
    for (int i = 1; i <= vertex_num - 1; i++)
    {
        for (int j = 0; j < edge_num; j++)
        {
            if (dist[edge[j].v] > dist[edge[j].u] + edge[j].w)
            {
                dist[edge[j].v] = dist[edge[j].u] + edge[j].w;
                path[edge[j].v] = edge[j].u;
            }
        }
    }

    bool flag = true;  //标记是否有负权回路

    //第n次循环判断负权回路
    for (int i = 0; i < edge_num; i++)
    {
        if (dist[edge[i].v] > dist[edge[i].u] + edge[i].w)
        {
            flag = false;
            break;
        }
    }

    return flag;
}

void Print()
{
    for (int i = 0; i < vertex_num; i++)
    {
        if (i != source)
        {
            int p = i;
            stack<int> s;
            cout << "顶点 " << source << " 到顶点 " << p << " 的最短路径是： ";

            while (source != p)  //路径顺序是逆向的，所以先保存到栈
            {
                s.push(p);
                p = path[p];
            }

            cout << source;
            while (!s.empty())  //依次从栈中取出的才是正序路径
            {
                cout << "--" << s.top();
                s.pop();
            }
            cout << "    最短路径长度是：" << dist[i] << endl;
        }

    }
}

int main()
{

    cout << "请输入图的顶点数，边数，源点：";
    cin >> vertex_num >> edge_num >> source;

    cout << "请输入" << edge_num << "条边的信息：\n";
    for (int i = 0; i < edge_num; i++)
        cin >> edge[i].u >> edge[i].v >> edge[i].w;

    if (BellmanFord())
        Print();
    else
        cout << "Sorry,it have negative circle!\n";

    return 0;
}

运行截图：