三分题两道：lightoj1146 Closest Distance、lightoj1240 Point Segment Distance (3D)

lightoj1146

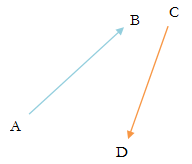
Two men are moving concurrently, one man is moving from A to B and other man is moving from C to D. Initially the first man is at A, and the second man is at C. They maintain constant velocities such that when the first man reaches B, at the same time the second man reaches D. You can assume that A, B, C and D are 2D Cartesian co-ordinates. You have to find the minimum Euclidean distance between them along their path.

 

Input
Input starts with an integer T (≤ 1000), denoting the number of test cases.

Each case will contain eight integers: Ax, Ay, Bx, By, Cx, Cy, Dx, Dy. All the co-ordinates are between 0 and 100. (Ax, Ay) denotes A. (Bx, By) denotes B and so on.

Output
For each case, print the case number and the minimum distance between them along their path. Errors less than 10-6 will be ignored.

Sample Input
3
0 0 5 0 5 5 5 0
0 0 5 5 10 10 6 6
0 0 5 0 10 1 1 1

Output for Sample Input
Case 1: 0
Case 2: 1.4142135624
Case 3: 1

题意：小明从A点出发走到B点，小红从C点出发走到D点，已知小明到达B点的同时小红到达D点，还有ABCD的坐标

求小明和小红之间的最近♂距离

题解：三分时间，如果mid1比mid2距离小。那么答案肯定在l~mid2中

反之则一定在mid1~r中

然后据此随便三分个1000次，答案也就符合精度了。

蜜汁尴尬的TLE

代码如下，也是难得这么短。

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int t,ttt=,ax,ay,bx,by,cx,cy,dx,dy,times;
double diss(double mid)
{
    double x1,y1,x2,y2;
    x1=ax+(bx-ax)*mid;
    y1=ay+(by-ay)*mid;
    x2=cx+(dx-cx)*mid;
    y2=cy+(dy-cy)*mid;
    return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        ttt++;
        scanf("%d%d%d%d%d%d%d%d",&ax,&ay,&bx,&by,&cx,&cy,&dx,&dy);
        double l=,r=,mid1,mid2;
        times=;
        while(times--)
        {
            mid1=(l+l+r)/;
            mid2=(l+r+r)/;
            double dis1=diss(mid1),dis2=diss(mid2);
            if(dis1<dis2)
            {
                r=mid2;
            }
            else
            {
                l=mid1;
            }
        }
        printf("Case %d: %.6lf\n",ttt,sqrt(diss(l)));
    }
}

lightoj1240

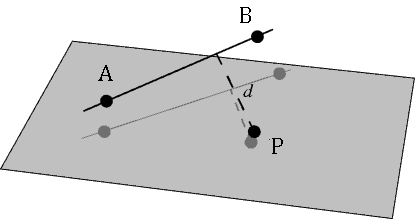
Given a segment in 3D space, identified by A(x1, y1, z1), B(x2, y2, z2) and another point P(x, y, z) your task is to find the minimum possible Euclidean distance between the point P and the segment AB.

 

Input
Input starts with an integer T (≤ 10000), denoting the number of test cases.

Each case starts with a line containing nine integers x1, y1, z1, x2, y2, z2, x, y, z. The magnitude of any integer will not be greater than 100.

Output
For each case, print the case number and the distance. Errors less than 10-6 will be ignored.

Sample Input
Output for Sample Input
2
0 0 1 0 1 1 0 1 0
0 0 0 1 1 1 0 0 1
Case 1: 1
Case 2: 0.8164965809

题意：给出三维平面上的一条线段和一个点

求点到该线段的最短距离。

题解：

这道题令学车中学的在下不胜尴尬啊，因为半个月前刚做过啊……

基础训练搬原题也是醉了。

之前是用平面几何的做法，只有70分

现在一看也是可以三分的。

同样假设一个人从A走到B

三分时间即可。

代码如下：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int t,ttt,ax,ay,az,bx,by,bz,px,py,pz,times;
double diss(double mid)
{
    double x1,y1,z1;
    x1=ax+(bx-ax)*mid;
    y1=ay+(by-ay)*mid;
    z1=az+(bz-az)*mid;
    return (px-x1)*(px-x1)+(py-y1)*(py-y1)+(pz-z1)*(pz-z1);
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        ttt++;
        scanf("%d%d%d%d%d%d%d%d%d",&ax,&ay,&az,&bx,&by,&bz,&px,&py,&pz);
        times=;
        double l=,r=,mid1,mid2;
        while(times--)
        {
            mid1=(l+l+r)/;
            mid2=(l+r+r)/;
            double dis1=diss(mid1),dis2=diss(mid2);
            if(dis1>dis2)
            {
                l=mid1;
            }
            else
            {
                r=mid2;
            }
        }
        printf("Case %d: %.6lf\n",ttt,sqrt(diss(l)));
    }
}