Codeforces 348B：Apple Tree（DFS+LCM+思维）

http://codeforces.com/contest/348/problem/B

题意：给一棵树，每个叶子结点有w[i]个苹果，每个子树的苹果数量为该子树所有叶子结点苹果数量之和，要使得每个结点的各个子树苹果数量相等，求至少需要拿走的苹果数量。

思路：一开始以为只要使得所有子树之和相同就行了。

 void dfs(int u, int fa) {
     int num = , mi = INF;
     for(int i = head[u]; ~i; i = edge[i].nxt) {
         int v = edge[i].v; if(v == fa) continue;
         dfs(v, u);
         sz[u] += sz[v]; num++; mi = mi > sz[v] ? sz[v] : mi;
     }
     //printf("%d : %lld - %d - %d\n", u, sz[u], mi, num);
     ans += sz[u] - mi * num;
     sz[u] = mi * num + w[u];
 }

后来看错误的样例，是没理解好题意。

例如这组样例：

10
0 9 5 0 0 0 0 0 9 7
7 5
8 1
1 5
4 3
2 4
4 7
7 9
10 6
6 8

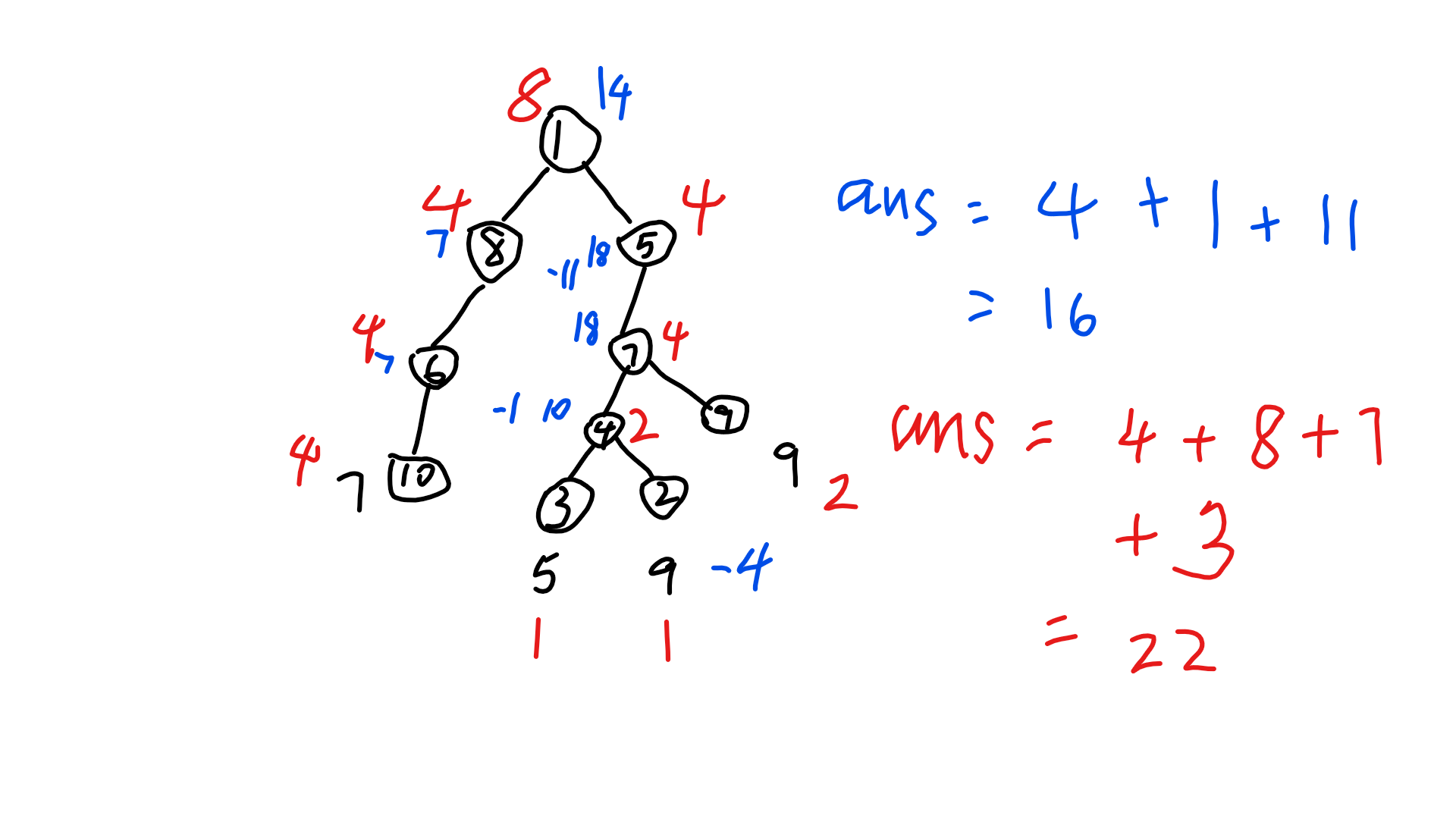红色的为正确的，蓝色为之前想错的。

题解：“对于一棵以u为根的子树，如果要减少若干个苹果，那么需要从u的每棵子树中取走等量的苹果，这个过程会递归下去直到叶子，
考虑对每个节点维护两个信息，mx[u]表示u子树中最多的苹果数，cnt[u]表示u子树中苹果数必须是cnt[u]的倍数，
如果u是叶子，那么有mx[u]=a[u]，cnt[u]=1，否则有cnt[u]=lcm(cnt[v])，这里v是u的儿子，mx[u]则是不超过min(mx[v])的最大的cnt[u]的倍数，
最后结果就是mx[1]，复杂度O(nlogA)，这个logA是gcd的复杂度。”

真的好厉害 = =

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define N 100010
 #define INF 0x3f3f3f3f
 struct Edge {
     int v, nxt;
 } edge[N*];
 LL w[N], ans, mx[N], cnt[N];
 int head[N], tot;
 void Add(int u, int v) {
     edge[tot] = (Edge) { v, head[u] }; head[u] = tot++;
     edge[tot] = (Edge) { u, head[v] }; head[v] = tot++;
 }

 LL gcd(LL a, LL b) { return b ? gcd(b, a % b) : a; }

 LL lcm(LL a, LL b) { return a / gcd(a, b) * b; }

 void dfs(int u, int fa) {
     int num = ;
     for(int i = head[u]; ~i; i = edge[i].nxt) {
         int v = edge[i].v; if(v == fa) continue;
         dfs(v, u);
         if(!num) mx[u] = mx[v], cnt[u] = cnt[v];
         else {
             if(cnt[u] < 1e14) cnt[u] = lcm(cnt[u], cnt[v]);
             mx[u] = min(mx[u], mx[v]) / cnt[u] * cnt[u]; // mx 必须是cnt[u]的倍数
         }
         num++;
     }
     if(!num) mx[u] = w[u], cnt[u] = ;
     else {
         mx[u] *= num;
         if(cnt[u] < 1e14) cnt[u] *= num;
     }
    // printf("%d : %lld - %lld\n", u, mx[u], cnt[u]);
 }

 int main() {
     int n; scanf("%d", &n); LL ans = ;
     for(int i = ; i <= n; i++) scanf("%lld", &w[i]), ans += w[i];
     memset(head, -, sizeof(head)); tot = ;
     for(int i = ; i < n; i++) {
         int u, v; scanf("%d%d", &u, &v); Add(u, v);
     }
     dfs(, -);
     cout << ans - mx[] << endl;
     return ;
 }