当我们在机器学习领域进行模型训练时,出现的误差是如何分类的?

我们首先来看一下,什么叫偏差(Bias),什么叫方差(Variance):

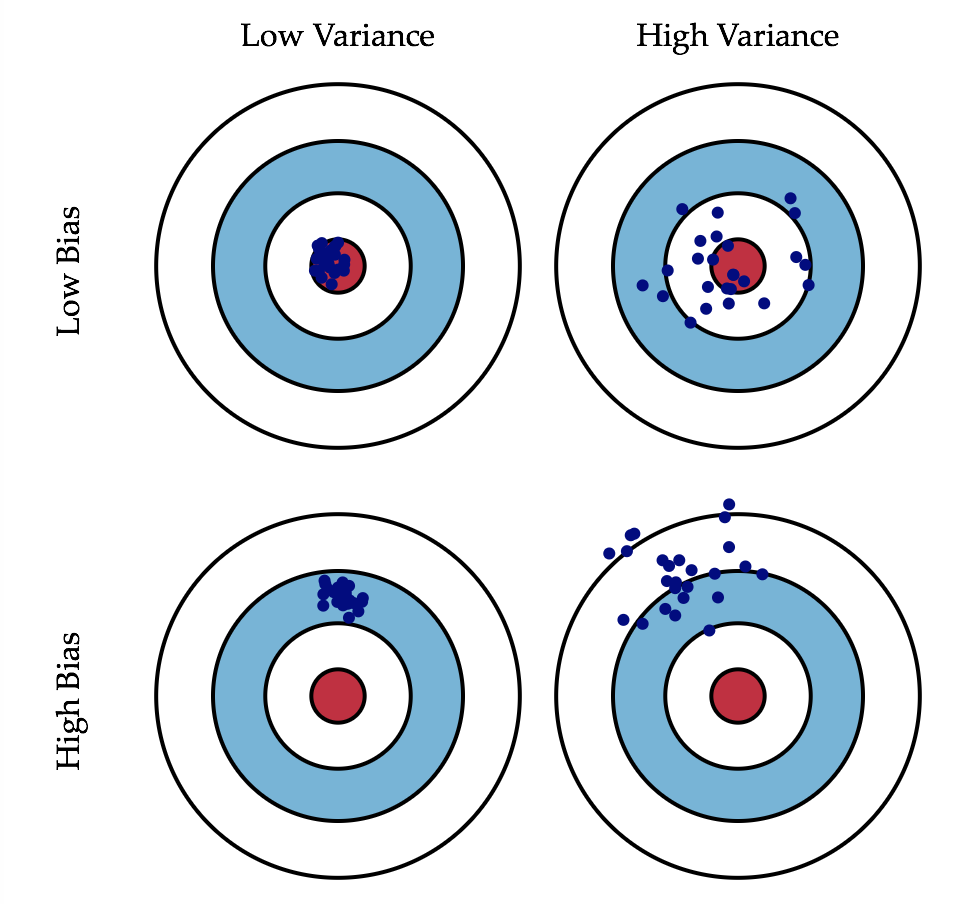
这是一张常见的靶心图

可以看左下角的这一张图,如果我们的目标是打靶子的话,我们所有的点全都完全的偏离了这个中心的位置,那么这种情况就叫做偏差

再看右上角这张图片,我么们的目标是右上角这张图片中心的红色位置,我们射击的点都围绕在这个红色的点的周围,没有大的偏差,但是各个点间过于分散不集中,就是有非常高的方差

我们进行机器学习的过程中，大家可以想象，我们实际要训练的那个模型都是要预测一个问题，这个问题本身我们就可以理解成是这个靶子的中心，而我们根据数据来拟合一个模型，进而预测这个问题，我们拟合的这个模型其实就是我们打出去的这些枪，那么我们的模型就有可能犯偏差和方差这样两种错误
 一般来说我们说我们训练一个模型，这个模型会有误差，这个误差通常来源于三方面 :

模型误差 = 偏差(Bias) + 方差(Variance) + 不可避免的误差

不可避免的误差: 客观存在的误差,例如采集的数据的噪音等,是我们无法避免的

 
偏差和方差这两个问题只是和我们的算法和我们训练的模型相关的两个问题，也就是说我们训练一个模型它有偏差，主要的原因就在于我们很有可能对这个问题本身的假设是不正确的，那么最典型的例子就是,如果我们针对非线性的数据或者说是非线性的问题，使用诸如线性回归这种现象的方法的话，那显然会产生非常高的偏差，那么在我们现实的环境中欠拟合(underfitting)就是这样的一个例子.

 还有典型的一个例子就是你训练数据所采用的那个特征，其实跟这个问题完全没有关系，比如说我们想预测一个学生的考试成绩，但是呢，我们是用这个学生的名字来预测他的考试成绩，那么显然一定是高偏差的，因为这个特征本身离我们要预测的那个问题的目标考试成绩之间是高度不相关的
 
方差在机器学习的过程中它的表现就在于数据的一点点的扰动都会极大的影响我们的模型，换句话说我们的模型没有完全的学习到这个问题的实质这个中心而学习到了很多的噪音，通常来讲我们的模型具有较高的方差的原因是我们的模型太过复杂，比如说高阶多项式回归这样的例子，过拟合(overfitting)就会极大的引入方差
 
  • 有一些算法天生是高方差的算法。如kNN,决策树等
  • 非参数学习通常都是高方差算法。因为不对数据进行任何假设
  • 有一些算法天生是高偏差算法。如线性回归
  • 参数学习通常都是高偏差算法。因为堆数据具有极强的假设

大多数算法具有相应的参数,可以调整偏差和方差, 比如kNN中的k和线性回归中使用多项式回归。

偏差和方差通常是矛盾的,我们要在两者之间找到一个平衡

在机器学习领域,主要的挑战来自方差,当然主要是在算法方面,实际问题中原因不尽相同

解决高方差的通常手段:

　　1.降低模型复杂度

　　2.减少数据维度;降噪

　　3.增加样本数

　　4.使用验证集

　　5.模型正则化

偏差和方差以及偏差方差权衡(Bias Variance Trade off)的更多相关文章

  1. 【笔记】偏差方差权衡 Bias Variance Trade off

    偏差方差权衡 Bias Variance Trade off 什么叫偏差,什么叫方差 根据下图来说 偏差可以看作为左下角的图片,意思就是目标为红点,但是没有一个命中,所有的点都偏离了 方差可以看作为右 ...

  2. 机器学习：偏差方差权衡（Bias Variance Trade off）

    一.什么是偏差和方差 偏差(Bias):结果偏离目标位置: 方差(Variance):数据的分布状态,数据分布越集中方差越低,越分散方差越高: 在机器学习中,实际要训练模型用来解决一个问题,问题本身可 ...

  3. [转]理解 Bias 与 Variance 之间的权衡----------bias variance tradeoff

    有监督学习中,预测误差的来源主要有两部分,分别为 bias 与 variance,模型的性能取决于 bias 与 variance 的 tradeoff ,理解 bias 与 variance 有助于 ...

  4. 斯坦福大学公开课机器学习： advice for applying machine learning | regularization and bais/variance（机器学习中方差和偏差如何相互影响、以及和算法的正则化之间的相互关系）

    算法正则化可以有效地防止过拟合, 但正则化跟算法的偏差和方差又有什么关系呢?下面主要讨论一下方差和偏差两者之间是如何相互影响的.以及和算法的正则化之间的相互关系 假如我们要对高阶的多项式进行拟合,为了 ...

  5. Error=Bias+Variance

    首先 Error = Bias + Variance Error反映的是整个模型的准确度,Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,Variance反映的是模型每一次输 ...

  6. Bias, Variance and the Trade-off

    偏差,方差以及两者权衡 偏差是由模型简化的假设,使目标函数更容易学习. 一般来说,参数化算法有很高的偏差,使它们学习起来更快,更容易理解,但通常不那么灵活.反过来,它们在复杂问题上的预测性能更低,无法 ...

  7. 机器学习总结-bias–variance tradeoff

    bias–variance tradeoff 通过机器学习,我们可以从历史数据学到一个\(f\),使得对新的数据\(x\),可以利用学到的\(f\)得到输出值\(f(x)\).设我们不知道的真实的\( ...

  8. 2.9 Model Selection and the Bias–Variance Tradeoff

    结论 模型复杂度↑Bias↓Variance↓ 例子 $y_i=f(x_i)+\epsilon_i,E(\epsilon_i)=0,Var(\epsilon_i)=\sigma^2$ 使用knn做预测 ...

  9. 训练/验证/测试集设置;偏差/方差;high bias/variance;正则化;为什么正则化可以减小过拟合

    1. 训练.验证.测试集 对于一个需要解决的问题的样本数据,在建立模型的过程中,我们会将问题的data划分为以下几个部分: 训练集(train set):用训练集对算法或模型进行训练过程: 验证集(d ...

随机推荐

  1. python爬虫笔记之re.match匹配，与search、findall区别

    为什么re.match匹配不到?re.match匹配规则怎样?(捕一下seo) re.match(pattern, string[, flags]) pattern为匹配规则,即输入正则表达式. st ...

  2. redis 发布与订阅原理分析

    前言:用了redis也有一段时间了,但是发布与订阅的使用频率也不高,趁着这次空闲,深究下redis的发布与订阅模式. 一.订阅频道和信息发布 功能说明:Redis 的 SUBSCRIBE 命令可以让客 ...

  3. HDU-1576 A/B 基础数论+解题报告

    HDU-1576 A/B 基础数论+解题报告 题意 求(A/B)%9973,但由于A很大,我们只给出n(n=A%9973) (我们给定的A必能被B整除,且gcd(B,9973) = 1). 输入 数据 ...

  4. 在springboot中使用swagger2

    1.在springboot中使用swagger的话,首先在pom文件中引入依赖 <!-- https://mvnrepository.com/artifact/io.springfox/spri ...

  5. C#的DateTime得到特定日期

    //指定时间 DateTime dt = new DateTime(2016, 6, 1); //当前时间 DateTime dt = DateTime.Now; //本周周一 DateTime st ...

  6. 带新手玩转MVC——不讲道理就是干（下）

    带新手玩转MVC——不讲道理就是干(下) 前言:废话不多说,直接开干 完整案例演示 案例代码 LoginServlet package servlet; import domain.User; imp ...

  7. idea新建javaweb工程

    最近尝试了idea的使用,将idea建立javaweb工程的步骤记录下来 1.方框里边是重点 2.next后输入工程文件名点击finish 3.如图看到项目文件夹里边没有WEB-INF文件夹及里边的w ...

  8. Linux/UNIX编程：使用C语言实现简单的 ls 命令

    刚好把 Linux/UNIX 编程中的文件和IO部分学完了,就想编写个 ls 命令练习一下,本以为很简单,调用个 stat 就完事了,没想到前前后后弄了七八个小时,90%的时间都用在格式化(像 ls ...

  9. 《JSP数据交互总结》

    1.1.1为什么需要动态网页 静态网页的内容是固定的,不能提供个性化和定制化的服务,因此,动态网页技术逐渐发展起来. 1.1.2什么是动态页面 动态网页是指在服务器端运行的使用程序语言设计的交互式网页 ...

  10. Jboss反序列化漏洞复现(CVE-2017-12149)

    Jboss反序列化漏洞复现(CVE-2017-12149) 一.漏洞描述 该漏洞为Java反序列化错误类型,存在于jboss的HttpInvoker组件中的ReadOnlyAccessFilter过滤 ...