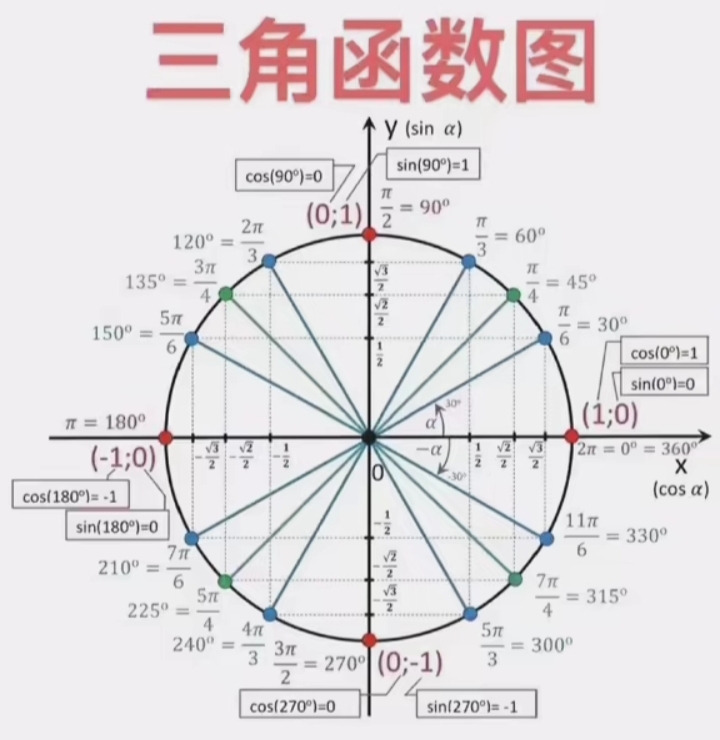
SciTech-Mathmatics-Trigonometric function三角函数-基础知识 + Number Theory数论 + Set Theory集合论{有限集(与自然数集1:1对应), 权势, 无限集}

1. 数论：

   • 在 周长为 \(1\pi\) (半径为1/2) 的圆上, 任选一点作为0点, 顺时针有序放置所有的\(\large N自然数\),
     
     Question: 什么情况会出现重合的两个自然数点 ？
     
     Solution:

     • Result: 任何两个自然数点(如此放置的), 任何条件(情况), 都不会重合(即使是无限多个自然数点序列).

     • Proof(反证法)：
       
       Hypothesis(假设):

       • 任取两个如此放置的自然数点为 \(\large a, b; a \in N, b \in N\) .
       • 存在\(\large a,\ b\)重合的情况:
         
         即\(\large (a - b) = k \cdot 2 \pi,\ where\ k \in N,\ and\ k \neq 0\) .
         
         $\large \therefore \frac{(a-b)}{2k} = \pi $
         
         \(\large \because \frac{(a-b)}{2k} \text{ is a Rational } and\ \pi \text{ is an Irrational}\)
         
         $\large \therefore \text{the left side } and \text{ the right side } \text{ will never be equal } $
         
         $\large \therefore \text{ contradicting with above hypothesis } $

       因此, “如此放置的任意两个自然数点”不存在“重合”的情况。
       
       同理, 如果：

       • 在“周长为\(\large \pi\) 的圆”上取“任何一点作为0点”，
       • 由0点开始, 在“顺时针”放置的所有“自然数点序列”取任何一点, 假设为 $\large a \in N $
       • 由0点开始, 在“逆时针”放置的所有“自然数点序列”取任何一点, 假设为 $\large b \in N $

       结果仍然是 $\large \text{a 与 b 永远不可能重合.} \(
       * 因为可将**“顺时针”放置的**所有“自然数点序列” 与 **“逆时针”放置的**所有“自然数点序列”,
       **分别看作“由同一0点开始放置的\)\large Z整数集\(”**的**“正半轴”**与**“负半轴”**。
       * 由之前" 顺时针放\)\large N自然数集\(" 情况的证明, 同理可证 "由0点开始放的\)\large Z整数集$"的情况.

2. 总图: