Day5 备战CCF-CSP练习

题目描述

给定 $n$ 个不同的整数，问这些数中有多少对整数，它们的值正好相差 $1$。

输出格式

输入的第一行包含一个整数 $n$，表示给定整数的个数。

第二行包含所给定的$ n$ 个整数。

输出格式

输出一个整数，表示值正好相差 $1$ 的数对的个数。

数据范围

$1≤n≤1000$,给定的整数为不超过 $10000$ 的非负整数。

输入样例：

6

10 2 6 3 7 8

输出样例：

样例解释

值正好相差 $1$ 的数对包括 $(2,3),(6,7),(7,8)$

。

题目分析

语法题

C++代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int n;

int a[N];

int res = 0;

int main()

{

    cin >> n;

    for(int i = 0 ; i < n ; i ++)

        cin >> a[i];

    for(int i = 0 ; i < n ; i ++)

        for(int j = i + 1 ; j < n ; j ++)

            if(abs(a[i] - a[j]) == 1)

                res ++ ;

    cout << res << '\n';

    return 0;

}

题目描述

在一个定义了直角坐标系的纸上，画一个 $(x_1,y_1)$ 到 $(x_2,y_2)$的矩形指将横坐标范围从 $x_1$ 到 $x_2$，纵坐标范围从 $y_1$ 到 $y_2$ 之间的区域涂上颜色。

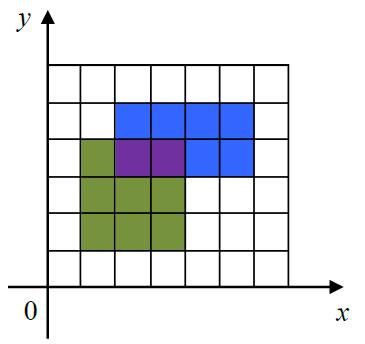
下图给出了一个画了两个矩形的例子。

第一个矩形是 $(1,1)$ 到 $(4,4)$，用绿色和紫色表示。

第二个矩形是 $(2,3)$ 到 $(6,5)$，用蓝色和紫色表示。

图中，一共有 $15$ 个单位的面积被涂上颜色，其中紫色部分被涂了两次，但在计算面积时只计算一次。

在实际的涂色过程中，所有的矩形都涂成统一的颜色，图中显示不同颜色仅为说明方便。

给出所有要画的矩形，请问总共有多少个单位的面积被涂上颜色。

输入格式

输入的第一行包含一个整数 $n$，表示要画的矩形的个数。

接下来 $n$ 行，每行 $4$个非负整数，分别表示要画的矩形的左下角的横坐标与纵坐标，以及右上角的横坐标与纵坐标。

输出格式

输出一个整数，表示有多少个单位的面积被涂上颜色。

数据范围

$1≤n≤100,0≤ 横坐标、纵坐标 ≤100$

输入样例：

输出样例：

题目分析

暴力/二维前缀和

暴力就不说了，讲一下优化

二位前缀和，我们将矩形中每一个点都当成前缀和的点，那么，我们只需要将顶点标注一下，就可以利用前缀和的性质画出整个矩形

如图一，蓝色是要画的目标矩形

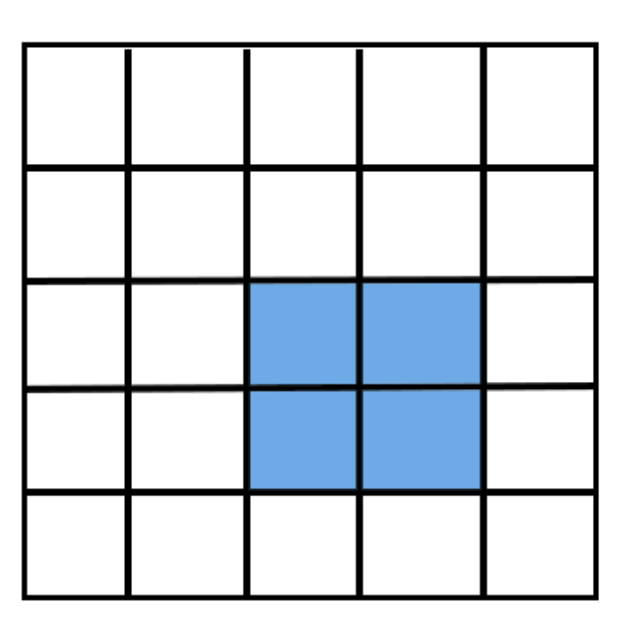
那么怎么构建差分数组呢

根据前缀和公式f[i][j] = f[i][j - 1] + f[i - 1][j] - f[i - 1][j - 1] + a[i][j]

其中f[i][j - 1] + f[i - 1][j] - f[i - 1][j - 1]都是以$(i , j)$为最右下的顶点的矩形面积（差分数组的矩形），问题是我们怎么通过控制顶点的a[i][j]来控制矩阵的大小。

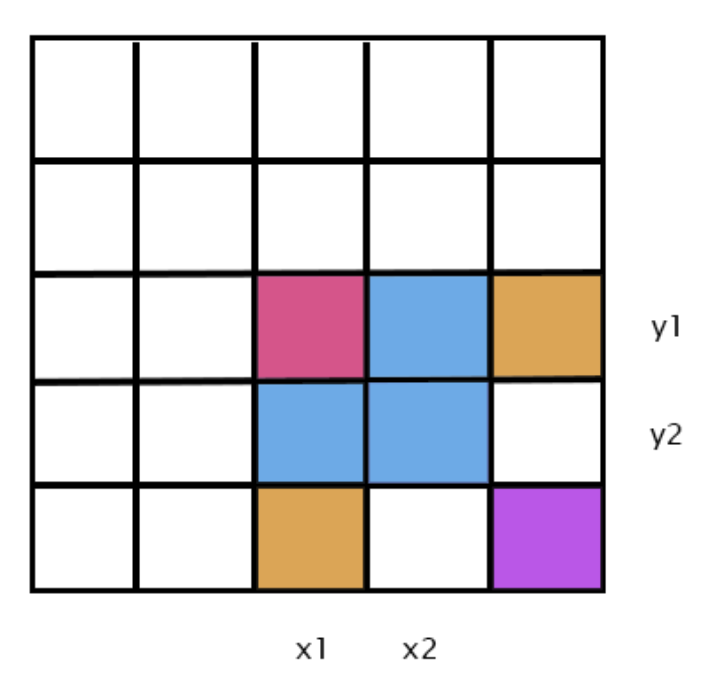
红色点是矩形的左上角，在此之前的所有点都为$0$，那么前缀和自然也为$0$，那么a[x1][y1] = 1，到了橘色点，矩形已经结束了，可是前缀和依然为$1$，因此a[x2 + 1][y1] = -1，同理另一个橘色点a[x1][y2 + 1] = -1 ，到了紫色点，由于两个橘色点，紫色点的前缀和为$-1$，所以a[x2 + 1][y2 + 1] = 1

然后推广就可以了，利用前缀和性质，只要不是$0$的点就是覆盖的点，求面积即可

构造差分数组 $\rightarrow$ 前缀和构建矩形 $\rightarrow$ 再次前缀和求覆盖面积

C++ 代码

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int f[N][N];

int n;

int main()

{

    cin >> n;

    while (n -- )

    {

        int a , b , x , y;

        cin >> a >> b >> x >> y;

        a ++ , b ++ ;

        f[a][b] += 1;

        f[x + 1][b] -= 1 , f[a][y + 1] -= 1;

        f[x + 1][y + 1] += 1;

    }

    for(int i = 1 ; i < N ; i ++)

        for(int j = 1 ; j < N ; j ++)

            f[i][j] += f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];

    for(int i = 1 ; i < N ; i ++)

        for(int j = 1 ; j < N ; j ++){

            if(f[i][j]) f[i][j] = 1;

            f[i][j] += f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];

        }    

    cout << f[N - 1][N - 1];        

}