AB Test基础与Python实战（一）：AB test介绍与原理

AB testing介绍

在日常的工作我们经常会遇到一些难以抉择的问题：在营销中如果有两个营销方案哪个更能吸引客户点击参与？在产品中现在我们有两个不同的界面，那个界面更符合大众使用习惯？

而这些方案的选择不能够仅仅拍脑袋决定，万一反馈不是很好，流失了用户或者减少了收入，其实对于公司来说，都是巨大的损失。因此需AB testing这样的方法去做一个实验，在相同的条件下控制单个变量（也就是所谓的对照实验）看两个方案之间的效果是否有差异，这样就可以把风险降到最低。通过AB Testing我们将决策由拍脑袋的方式使转变为数据驱动的方式，来帮助分析我们的产品，分析我们的用户反馈。

现在的问题是如何设计实验呢？直接选一堆人做实验相互比较结果的大小就行了吗？假设我们统计了1000人的数据，得出新版本的方案比旧版本带来的点击率提高了3%，那么这能证明新版本比旧版本更好吗？答案是不一定的，因为统计样本得到的数据是有波动的，如果日常点击率的波动就在正负5%左右，那么新版本点击率提高了3%完全有可能是因为波动引起的。所以在整个AB test过程中我们需要了解一些统计学知识，有对应基础的可以跳过这一部分。

基本原理

在AB testing中会用到一些的统计学原理，在这篇文章中只会大致描述下相关结论，具体推导和细节可以查看过往的文章：
概率论与数理统计常见的分布与性质：https://blog.csdn.net/qq_42692386/article/details/135251476
常见统计量与其抽样分布https://blog.csdn.net/qq_42692386/article/details/142366733
区间估计https://blog.csdn.net/qq_42692386/article/details/142203585
假设检验https://blog.csdn.net/qq_42692386/article/details/142549079
样本量的确定https://blog.csdn.net/qq_42692386/article/details/144735386

大数定理

大数定理：当试验条件不变时，随机试验重复多次以后，随机事件的频率近似等于随机事件的概率。
例如，观察个别或少数家庭的婴儿出生情况，发现有的生男，有的生女，没有一定的规律性，但是通过大量的观察就会发现，男婴和女婴占婴儿总数的比重均会趋于50%。
大数定理告诉我们能用频率近似代替概率；能用样本均值近似代替总体均值。在实际的统计应用中，我们一般无法获得总体的所有数据，所以都是通过抽取一些样本来进行研究，大数定理告诉我们对一定的样本数据就可以近似于对总体研究.

中心极限定理

设从均值为

μ，方差为

σ^2

σ2的任意一个总体中，抽取样本量为

n的样本。当

n充分大的时候，样本均值

\bar x

xˉ近似服从均值为

μ，方差为

σ²/n

σ2/n的正态分布。

∼

(

)

，即

−

∼

(

)

\bar{x} \sim N(μ,\frac{σ²}{n})，即\frac{\bar{x} - μ}{\sigma/\sqrt{n} } \sim N(0,1)

xˉ∼N(μ,nσ2)，即σ/n

xˉ−μ∼N(0,1)

中心极限定理告诉我们无论是什么分布的随机变量，在样本量足够的情况下都为正态分布。如下图反映了样本量变大的情况下分布的变化：

中心极限定理要求样本量充分大，但是多大才叫充分大呢？一般在统计学中n>=30称之为大样本(统计学中的一种经验说法)。因此在实际应用中一般都是大样本，都是服从正态分布的。

假设检验

详细介绍可参考相关文章，分别介绍区间估计https://blog.csdn.net/qq_42692386/article/details/142203585和假设检验https://blog.csdn.net/qq_42692386/article/details/142549079

假设检验，也称为显著性检验，是对总体特征做某种假设，然后通过样本统计量对此假设做出接受或者拒绝的判断。

举个例子来说：现在我想要判断一枚硬币的两边重量是否相同，那么我们可以设计一个实验：我们不停的抛这一枚硬币，然后记录其正反面的情况。如果统计结果是正反面的概率接近50%，那么我们可以判断这枚硬币的两边重量是相同的。同理，如果正面出现的概率是20%，而反面出现的概率是80%，那么我们有理由怀疑这枚硬币的正面和反面重量不同。

零假设与备选假设

在假设检验中通常会提出两个假设：零假设（也称为原假设，记为

H_0

H0）和备选假设（记为

H_1

H1）。零假设（

H_0

H0）是我们想通过实验反对的假设，例如上述抛硬币的例子中零假设就是硬币的两边重量是不同的，备选假设（

H_1

H1）是我们想通过实验证明的假设，例如硬币的两边重量是相同的。这样在一个假设检验中，零假设和备选假设相互对应，两者中有且仅有一个成立。
在AB test中，零假设一般为：AB组指标无显著差异，而备选假设为：AB组指标有明显差异。

显著性水平

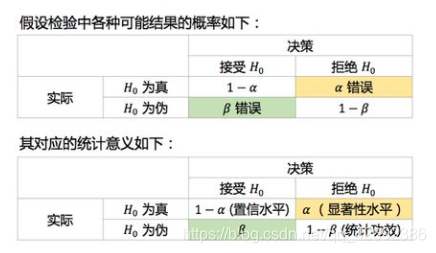
之前我们说过假设检验是通过样本统计量来判断提出的假设是否正确，因此我们可能会判断出错：当硬币的两边重量不相同时我们错误的判断硬币的两边重量相同，也有可能是硬币的两边重量相同时我们错误的判断硬币的两边重量不相同。这对应统计学中两种错误：

第一类错误：当

H_0

H0为真时，我们拒绝了

H_0

H0，发生的概率为

α
第二类错误：当

H_0

H0为假时，我们却接受了

H_0

H0，发生的概率为

而显著性水平就是指一类错误的概率，通常显著性水平用α表示。在统计学中，一般统计学中α可以取0.05或者0.01,它表示犯一类错误的概率为5%和1%。

拒绝域与单侧双侧检验

根据显著性水平可以计算出合理区间与不合理的区间，例如抛硬币正反面的概率在45%到55%，那么我们可以认为这枚硬币的两边重量是相同的。如果在这个区间外就认为差距过大不合理，认为这枚硬币的两边重量不相同。这个算出来的“不合理区间”就是拒绝域。如果样本观测计算出来的检验统计量的具体数值落在拒绝域内，就拒绝原假设，否则不拒绝原假设。给定显著性水平α后，查表就可以得到具体临界值，将检验统计量与临界值进行比较，判断是否拒绝原假设。

单侧检验与双侧检验

在进行假设检验时，检验方式分为两种：双侧检验和单侧检验。

双侧检验： 如果检验的目的是检验抽样的样本统计量与假设参数的差是否过大（没有特定的方向性，形式类似为“≠”这种），我们都会把风险分摊到左右两侧。比如显著性水平为5%，则概率曲线的左右两侧各占2.5%，也就是95%的置信区间。
单侧检验： 如果检验的目的只是注重验证是否偏高，或者偏低，也就是说只注重验证单一方向，我们就检验单侧（形式为">“或”<"的假设检验，称为单侧检验.其中 "<“称为左侧检验，”>"称为右侧检验。）。比如显著性水平为5%，概率曲线只需要关注某一侧占5%即可，即90%的置信区间。

在实践中，我们会根据问题的性质来决定采用双侧检验还是单侧检验

举个例子，同样是检验中学生男女生身高是否有性别差异。如果问题是：中学生中，男女生的身高是否存在性别差异，这个时候我们需要用双侧检验，因为实际的差异可能是男生平均身高比女生高，也可能是男生平均比女生矮。这两种情况都属于存在性别差异。而如果问题变为：中学生中，男生的身高是否比女生高，这个时候我们只需要检验单侧即可。

P-Value(P值)

P值定义为当原假设为真时，所获得的样本结果至少与实测结果不同的概率值，它通常又称为实测显著性水平。
接着用上面的抛硬币的例子来说。假设我的零假设是硬币的两面重量不一样，算出来的P值0.04，那么也就是说是在零假设（硬币的两面重量不一样）成立的前提下，我们通过抽样得到这样一个样本数据的可能性是4%

那么，0.04 这个概率或者说显著性水平到底是大还是小，够还是不够用来拒绝原假设呢？这就需要把 p 和显著性水平，也就是我们上面说的第 I 类错误的小概率标准 α 来比较确定。假设检验的决策规则：

若

p

≤

α

p\leqα

p≤α，那么拒绝原假设；
若
p

>

α

p>α

p>α，那么不能拒绝原假设。

如果 α 取 0.05 而 p = 0.04，说明如果原假设为真，则此次试验发生了小概率事件。根据小概率事件不会发生的判断依据，我们可以反证认为原假设不成立。

样本量的确定

在实际的AB testing中，确定实验对于样本量大小的需求也是是很重要的一步。理论上来说样本量越大越好，因为样本量很少的情况下，实验结果可能被异常样本带偏，最终可能得到不准确的结果。但是使用样本量太大，相应的试错成本也会增大。

举个例子来说，我们拿所有的用户来跑AB testing，但不幸的是，1周后结果表明实验组的总收入下降了20%或者用户流失了20%，这样我们知道了实验组的效果不好，但是这个结论的代价是一周内给整个公司带来了20%的损失或者20%的用户流失。

因此我们需要找到一个最小的测试样本量，这个样本量可以在满足实验的可信度的要求的同时减少我们的试错成本。

一般情况下我们都是直接使用计算器直接计算样本量的。常用的计算器有：
1.数值类计算：需要填写方差
http://powerandsamplesize.com/Calculators/Compare-2-Means/2-Sample-Equality
https://www.stat.ubc.ca/~rollin/stats/ssize/n2.html2

比值类计算：不需要方差
https://www.evanmiller.org/ab-testing/sample-size.html
https://abtestguide.com/abtests

evanmiller工具对应的使用方法可以参考https://blog.csdn.net/qq_42692386/article/details/145571880

接下来讲一下具体的最小样本量计算公式。
在之前已经说过具体的OC函数与样本量计算的推导，由中心极限定理一般我们的样本都服从正态分布，所以基本上使用的是Z检验。
双侧最小样本量的公式：

(

)

n=\frac{\sigma^2}{\Delta^2}(Z_{\alpha/2}+Z_{\beta})^2

n=Δ2σ2(Zα/2+Zβ)2
单侧最小样本量的公式：

(

)

n=\frac{\sigma^2}{\Delta^2}(Z_{\alpha}+Z_{\beta})^2

n=Δ2σ2(Zα+Zβ)2
说明：
（1）

n 是每组所需样本量，因为 A/B 测试一般至少 2 组，所以实验所需样本量为 2n；
（2）

\alpha

α 和

\beta

β 分别称为第一类错误概率和第二类错误概率，一般分别取 0.05 和 0.2；
（3）

Z 为正态分布的分位数函数；
（4）

\Delta

Δ为两组数值的差异，如注册人数从 50到 60，那么

\Delta

Δ就是 10，在一些公式中表示为均值差

−

\mu_1-\mu_2

μ1−μ2；
（5）

\sigma

σ为标准差，是数值波动性的衡量，

\sigma

σ越大表示数值波动越厉害。

实际A/B测试中，我们关注的较多的一类是比例类的数值，如点击率、转化率等。这类比例类数值的特点是，对于某一个用户（样本中的每一个样本点）其结果只有两种，“成功”或“未成功”；对于整体来说，其数值为结果是“成功”的用户数所占比例。如转化率，对于某个用户只有成功转化或未成功转化。比例类数值的假设检验在统计学中叫做两样本比例假设检验。其最小样本量计算的公式为：

(

⋅

(

)

⋅

(

−

(

)

⋅

(

−

)

⋅

(

−

)

∣

−

∣

n = \frac{(Z_{\frac{\alpha }{2}} \cdot \sqrt{2\cdot \frac{(p_1+p_2)}{2}\cdot (1-\frac{(p_1+p_2)}{2})}+Z_{\beta }\cdot \sqrt{p_1\cdot (1-p_1) + p_2\cdot (1-p_2)})^2}{|p_1-p_2|^2}

n=∣p1−p2∣2(Z2α⋅2⋅2(p1+p2)⋅(1−2(p1+p2))

+Zβ⋅p1⋅(1−p1)+p2⋅(1−p2)

)2
上面式子中p1我们称为基础值，是实验关注的关键指标现在的数值（对照组）；p2我们称为目标值或者是结果值，是希望通过实验将其改善至的水平,

同时我们还可以使用Pythonh或者R代码直接计算

from statsmodels.stats.power import zt_ind_solve_power

from statsmodels.stats.proportion import proportion_effectsize as es

print(zt_ind_solve_power(effect_size=es(prop1=0.2, prop2=0.25), alpha=0.05, power=0.8, alternative="two-sided"))

参考文章：
https://jeffshow.com/caculate-abtest-required-sample-size.html
https://zhuanlan.zhihu.com/p/148760397
https://zhuanlan.zhihu.com/p/148760397