day4-进制与位运算

进制

对于整数有4种表现方式

• 二进制,满二进一
• 十进制,满10进1
• 八进制,满8进1,数字0开头
• 十六进制,满16进1,以0x或0X开头

进制转换

二进制转十进制

规则:从最低位开始(右边),将每位数提取出来,乘以2的(位数-1)次方,然后求和
1011 = 2^0 + 2^1 + 0 + 2^3 = 11
110001100 = 4 + 8 + 2^7 + 2^8  = 128 +256 +4 +8 =396

二进制转八进制

规则:将二进制的每三位一组(从最右边),转成对应的八进制数即可
11010101 = (11)(010)(101) = 0325
11100101 = (11)(100)(101) = 0345

二进制转十六进制

规则:将二进制的每四位一组(从最右边),转成对应的十六进制数即可
11010101 = (1101)(0101) = 0xd5
1110010110 = (11)(1001)(0110) = 0x396

八进制转十进制

规则:从最低位开始(右边),将每位数提取出来,乘以8的(位数-1)次方,然后求和
0123 = 3 * 8^0 + 2 * 8^1  + 1* 8^2 = 3+16+64 = 83
02456 = 6 + 40 + 64*4 +2*8^3 = 1024 + 256 + 46 = 1326

八进制转二进制

规则:将八进制的每一位数转化成对应3位数的二进制即可
0237 = (010)(011)(111)

十六进制转十进制

规则:从最低位开始(右边),将每位数提取出来,乘以16的(位数-1)次方,然后求和
0X34A = 10 * 16^0 + 4 * 16^1 + 3 * 16^2 = 10 + 64 + 768 = 842
0xA45 = 5 + 64 + 10 * 16^2 = 2560+ 69 = 2629

十六进制转二进制

规则:将十六进制的每一位数转化成对应4位数的二进制即可
0x237 = (0010)(0011)(0111)

十进制转二进制

规则:将该数不断除以2,直到商为0为止,将每部对应的余数倒过来就是对应二进制
56 = 111000
123 = 1111011

十进制转八进制

规则:将该数不断除以8,直到商为0为止,将每部对应的余数倒过来就是对应二进制
156 = 0234
678 = 1246

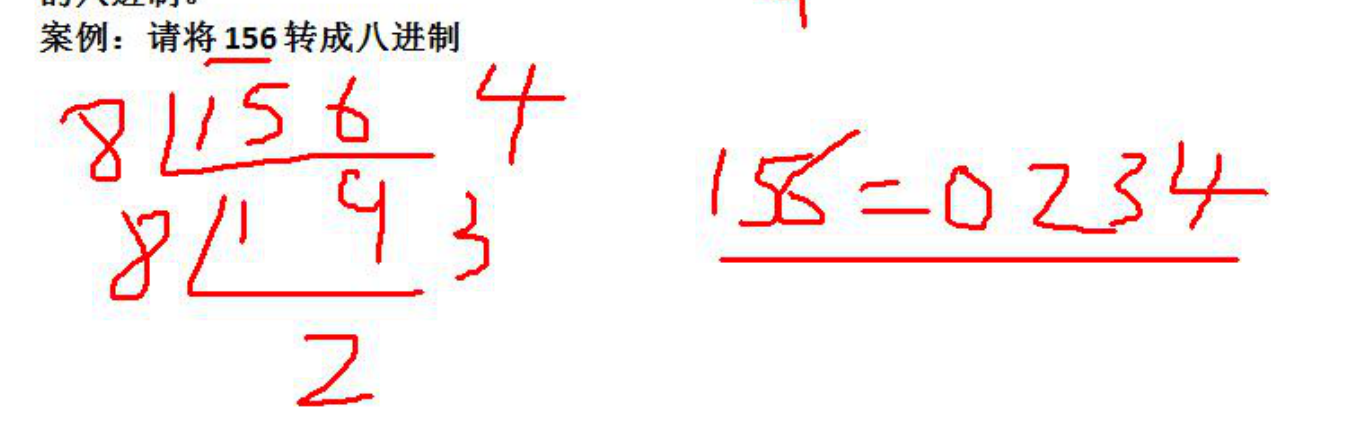
十进制转十六进制

规则:将该数不断除以16,直到商为0为止,将每部对应的余数倒过来就是对应二进制
356 =  0x164
8912 = 0X22d0

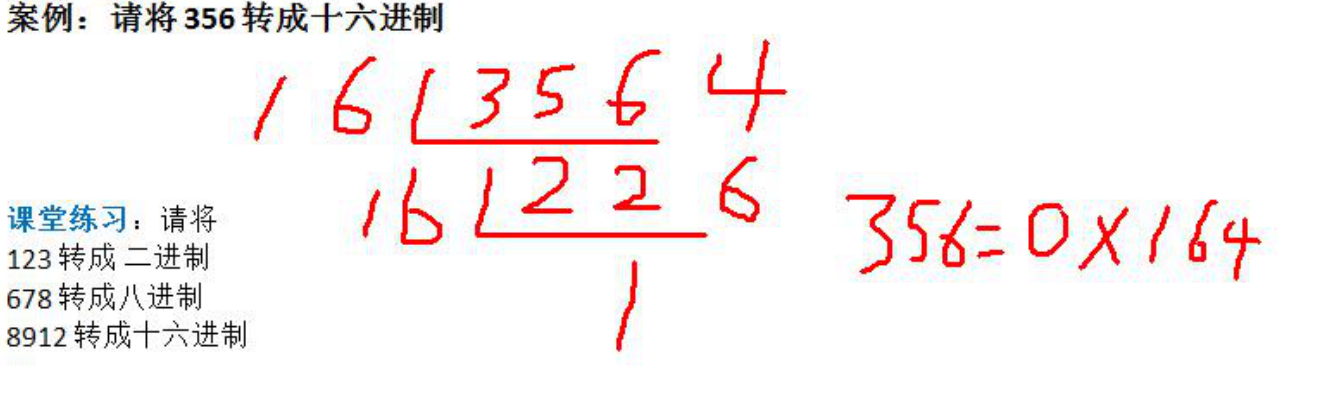
位运算

二进制的运算

在计算机内部,运行各种计算时,都是以二进制的方式运行

原码、反码、补码

1. 对于有符号的而言,二进制的最高位是符号为,0为整数,1为负数
2. 正数的原码、反码、补码都一样
3. 负数的反码,符号位不变,其他位取反
4. 负数的补码,等于反码+1
5. 0的反码补码都是0
6. 计算机运行的时候,都是以补码的方式运行的

1  -》 原码0000 0001 =》反码=》0000 0001=》补码0000 0001
-1 =》 源码1000 0001 =》反码=》1111 1110=》补码1111 1111

位运算符和移位运算符

3个位运算

1. 按位与& : 2位为1,结果为1,反之为0
2. 按位或| : 2位其中一位为1,结果为1,反之为0
3. 按位异或^ : 两个相同为0,不同为1

2个移位运算符

1. 左移<< 符号位不变,低位补0
2. 右移>>符号位不变,低位溢出,并用符号为补溢出的高位

a := 1 >> 2 // 0000 0001 => 0000 0000 = 0
b := 1 << 2 // 0000 0001 => 0000 0100 = 4

思考题

1) 请看下面的代码段，回答 a,b,c,d 结果是多少?
func main() {
    var a int = 1 >> 2
    var b int = -1 >> 2
    var c int = 1 << 2
    var d int = -1 << 2 

    //a,b,c,d 结果是多少
    fmt.Println("a=", a)  //0
    fmt.Println("b=", b)  //-1
    fmt.Println("c=", c)  //4
    fmt.Println("d=", d)  //-4
}

1 >> 2 // 0000 0001 => 0000 0000 = 0
-1 >> 2 // 1000 0001原码 =》反码 1111 1110=》补码 1111 1111 >>2 = 1111 1111 补码=》反码1111 1110 =》 1000 0001 = -1
1 << 2 // 0000 0001 => 0000 0100 = 4
-1 << 2  // 1111 1111补码=》1111 1100 =》反码=》1111 1011 =》原码 1000 0100 = -4

2) 请回答在 Golang 中，下面的表达式运算的结果是:
func main() {
    fmt.Println(2&3) //2
    fmt.Println(2|3) //3
    fmt.Println(13&7) //5
    fmt.Println(5|4) //5
    fmt.Println(-3^3) //-2
}

2&3 0000 0010
    0000 0011
    0000 0010 = 2

2|3 0000 0010
    0000 0011
    0000 0011 = 3

13&7 0000 1101
     0000 0111
     0000 0101 =5

5|4 0000 0101
    0000 0100
    0000 0101 = 5

-3^3 1111 1101
     0000 0011
     1111 1110补码 =》1111 1101反码 =》 1000 0010 = -2
-3 =》 1000 0011原码=》反码 1111 1100 =》补码1111 1101