动态规划-Race Car

2018-10-26 21:06:54

问题描述：

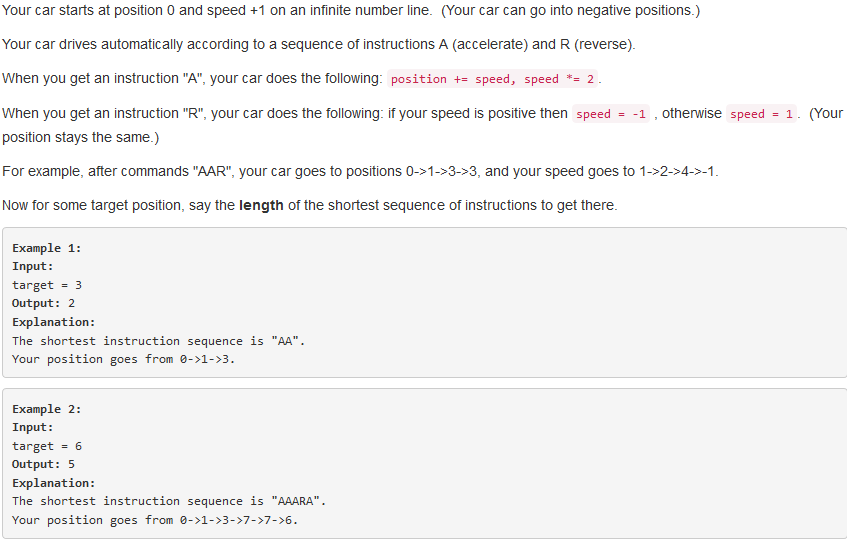
问题求解：

方法一、BFS

首先将使用BFS进行解空间的遍历，也就是将本问题转化成了搜索问题，但是有两个地方需要注意：

1、状态保存的问题，每个位置的状态由其位置信息和速度信息构成，但是如果将所有的位置出现过的速度进行保存会MLE，这里进行了一步简化，只保存当前位置速度绝对值为1的状态，定义这些状态不再后续的求解中被重复扩展；

2、Pruning，必须剪枝，如果不剪枝，则会TLE，这里采取的剪枝策略是将所有扩展到的距离target长度大于target的pos放弃。

3、状态保存采用了字符串拼接，这里可以进行进一步的优化。

    public int racecar(int target) {
        int step = 0;
        Queue<int[]> q = new LinkedList<>();
        q.add(new int[]{0, 1});
        Set<String> set = new HashSet();
        set.add("0_1");
        set.add("0_-1");
        while (!q.isEmpty()) {
            step++;
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int[] cur = q.poll();
                int pos = cur[0] + cur[1];
                int speed = cur[1] * 2;
                if (pos == target) return step;
                if (Math.abs(pos - target) < target)
                    q.add(new int[]{pos, speed});
                pos = cur[0];
                speed = cur[1] > 0 ? -1 : 1;
                String state = String.valueOf(pos) + "_" + String.valueOf(speed);
                if (set.contains(state)) continue;
                set.add(state);
                q.add(new int[]{pos, speed});
            }
        }
        return -1;
    }

方法二、BFS + Integer状态

使用String来保存状态，在每次用Hash查询的时候开销非常大，这里可以使用Integer来进行优化。时间是原来是1/4，应该来说速度上提升还是很多的。

    public int racecar(int target) {
        int step = 0;
        Queue<int[]> q = new LinkedList<>();
        q.add(new int[]{0, 1});
        Set<Integer> set = new HashSet();
        set.add(0 << 2 | 1);
        set.add(0 << 2 | 2);
        while (!q.isEmpty()) {
            step++;
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int[] cur = q.poll();
                int pos = cur[0] + cur[1];
                int speed = cur[1] * 2;
                if (pos == target) return step;
                if (Math.abs(pos - target) < target)
                    q.add(new int[]{pos, speed});
                pos = cur[0];
                speed = cur[1] > 0 ? -1 : 1;
                Integer state = pos << 2 | ((speed == 1) ? 1 : 2);
                if (set.contains(state)) continue;
                set.add(state);
                q.add(new int[]{pos, speed});
            }
        }
        return -1;
    }

方法三、DP

本题使用DP是最优解。

dp[i] : 在位置i的最短步数

有一个特殊情况，就是当前的pos正好等于2 ^ n - 1，此时所需步数可以直接运算出来，即d[i] = n    if i == 2 ^ n - 1

如果当前的pos不是最佳情况，那么就有两种策略，一是先经过pos，在往回倒，二是在到达之前进行倒车再前进。

算法的时间复杂度分析：总的状态数为t，每个状态求解的均摊时间在logt，所以时间复杂度为O(nlogn)。使用Java运行时间为3ms，beat 100%。

    public int racecar(int target) {
        int[] dp = new int[target + 1];
        return helper(target, dp);
    }

    private int helper(int target, int[] dp) {
        if (dp[target] != 0) return dp[target];
        int n = (int) Math.ceil(Math.log(target + 1) / Math.log(2));
        if (1 << n == target + 1) return dp[target] = n;
        dp[target] = n + 1 + helper((1 << n) - 1 - target, dp);
        for (int m = 0; m < n - 1; m++) {
            int pos = (1 << (n - 1)) - (1 << m);
            dp[target] = Math.min(dp[target], n + m + 1 + helper(target - pos, dp));
        }
        return dp[target];
    }