Bellman-Ford算法——为什么要循环n-1次？图有n个点，又不能有回路，所以最短路径最多n-1边。又因为每次循环，至少relax一边所以最多n-1次就行了！

单源最短路径

给定一个图,和一个源顶点src,找到从src到其它所有所有顶点的最短路径，图中可能含有负权值的边。

Dijksra的算法是一个贪婪算法,时间复杂度是O(VLogV)(使用最小堆)。但是迪杰斯特拉算法在有负权值边的图中不适用,Bellman-Ford适合这样的图。在网络路由中，该算法会被用作距离向量路由算法。Bellman-Ford也比迪杰斯特拉算法更简单。但Bellman-Ford的时间复杂度是O(VE),这要比迪杰斯特拉算法慢。（V为顶点的个数,E为边的个数）

算法描述

输入:图 和 源顶点
输出:从src到所有顶点的最短距离。如果有负权回路(不是负权值的边),则不计算该最短距离，没有意义，因为可以穿越负权回路任意次，则最终为负无穷。

算法步骤

1.初始化：将除源点外的所有顶点的最短距离估计值 dist[v] ← +∞, dist[s] ←0;
2.迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行|v|-1次）
3.检验负权回路：判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回false，表明问题无解；否则算法返回true，并且从源点可达的顶点v的最短距离保存在 dist[v]中。

关于该算法的证明也比较简单，采用反证法，具体参考：http://courses.csail.mit.edu/6.006/spring11/lectures/lec15.pdf
该算法是利用动态规划的思想。该算法以自底向上的方式计算最短路径。
它首先计算最多一条边时的最短路径(对于所有顶点)。然后,计算最多两条边时的最短路径。外层循环需要执行|V|-1次。

例子

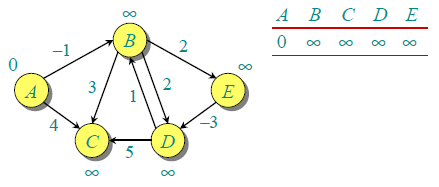
一下面的有向图为例：给定源顶点是0，初始化源顶点距离所有的顶点都是是无穷大的,除了源顶点本身。因为有5个顶点，因此所有的边需要处理4次。

按照以下的顺序处理所有的边：(B,E), (D,B), (B,D), (A,B), (A,C), (D,C), (B,C), (E,D).
第一次迭代得到如下的结果(第一行为初始化情况,最后一行为最终结果)：

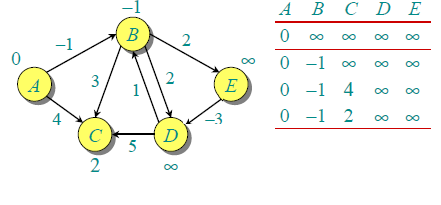
当 (B,E), (D,B), (B,D) 和 (A,B) 处理完后，得到的是第二行的结果。
当 (A,C) 处理完后，得到的是第三行的结果。
当 (D,C), (B,C) 和 (E,D) 处理完后，得到第四行的结果。

第一次迭代保证给所有最短路径最多只有1条边。当所有的边被第二次处理后，得到如下的结果(最后一行为最终结果)：

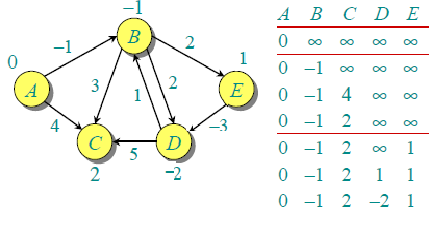
第二次迭代保证给所有最短路径最多只有2条边。我们还需要2次迭代(即所谓的松弛操作)，就可以得到最终结果。

算法描述

1,.初始化：将除源点外的所有顶点的最短距离估计值 d[v] ——>+∞, d[s]——>0;

2.迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行|v|-1次）

3.检验负权回路：判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回false，表明问题无解；否则算法返回true，并且从源点可达的顶点v的最短距离保存在 d[v]中。

为什么要循环V-1次？
答：因为最短路径肯定是个简单路径，不可能包含回路的，如果包含回路，且回路的权值和为正的，那么去掉这个回路，可以得到更短的路径如果回路的权值是负的，那么肯定没有解了.图有n个点，又不能有回路，所以最短路径最多n-1边。又因为每次循环，至少relax一边所以最多n-1次就行了。

算法导论上的伪代码：

BELLMAN-FORD(G, w, s)
1  INITIALIZE-SINGLE-SOURCE(G, s)
2  for i ← 1 to |V[G]| - 1
3       do for each edge (u, v) ∈ E[G]
4              do RELAX(u, v, w)
5  for each edge (u, v) ∈ E[G]
6       do if d[v] > d[u] + w(u, v)
7             then return FALSE
8  return TRUE