KKT条件原理

问题引入

max f(x, y)

s.t.

g(x,y) <= 0

几何解释

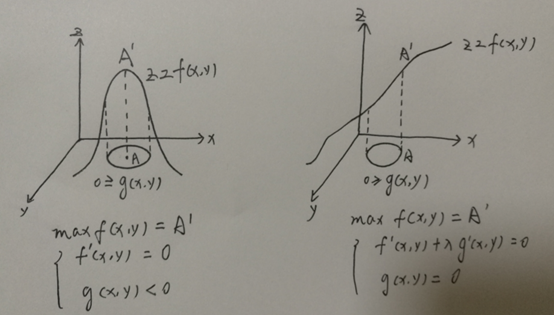
a.  g(x ,y) <= 0为上图中z = 0平面中的圆，圆的边表示g(x, y) = 0，圆的内部表示g(x, y) < 0。

b.  z = f(x, y)为上图中的曲面。

上述极值问题就是要求当点(x, y)落在圆内时（包括圆的边），f(x, y)的最大值。

1、    如果极值点在圆内，则显然有

f'(x, y) = 0

g(x, y) < 0

2、    如果极值点在圆边上，有拉格朗日乘子法我们知道

f’(x, y) + λg’(x ,y) = 0

g(x, y) = 0

如果是数学考试，我们直接求出上面两种情况的所有解(x, y)，再带入f(x, y)计算，选取最大值即可。

对偶问题

稍微修改一下文章开头的极值问题，得到新的极值问题1

min f(x, y)

s.t.

g(x,y) <= 0

拉格朗日函数如下

F(x, y, λ) = f(x, y) + λg(x, y)

我们对x, y求导数并令其为0，即

F’(x, y, λ) = f’(x, y) + λg’(x, y) = 0

场景1等价于

F’(x, y, λ) = 0

g(x, y) < 0

λ = 0

场景2等价于

F’(x, y, λ) = 0

g(x, y) = 0

λ > 0

场景二极小值点在圆边上，如果此时f(x, y)与g(x, y)梯度方向相同，说明点(x ,y)往圆内移动，f(x, y)的值会和g(x, y)的值一样减小，显然此时圆边上的点(x, y)不是极小值点。所以如果f(x, y)的极小值点在圆边上，必然f(x, y)与g(x, y)梯度方向相反，即λ > 0。

综合上述两种情况，极值问题1的对偶问题2如下（对偶问题解决了，原问题也就解决了）

max F(x, y, λ) = f(x, y) + λg(x, y)

s.t.

g(x, y) <= 0

λ >= 0

λg(x, y) = 0

点(x, y)在圆圈g(x, y) <= 0内，对于λ >= 0，我们有F(x, y, λ) <= f(x, y)，于是F(x, y, λ)的上界就是f(x, y)的下界。

我们把

g(X) <= 0

λ >= 0

λg(X) = 0

称作KKT条件。X表示向量(x1; x2; …; xn)。