Leetcode Sqrt(x)

参考Babylonian method

 （x0  越接近S的平方根越好）

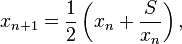
class Solution {
public:
    int sqrt(double x) {
        if(x == ) return ;
        double root = x/, tolerance = 1.0e-2;
        do{
            root=(root+x/root)/;
        }while(abs(root*root-x)>tolerance);
        return root;
    }
};

这题感觉题目有问题，返回的平方根竟然是整数，

另一种方法是是用二分搜索

class Solution {
public:
    int sqrt(int x) {
        if(x < ) return x;
        int left = , right = x;
        while(left <= right){
            int mid = (right+left)/;
            if(mid < x/mid) left = mid+;
            else if(x/mid < mid ) right = mid-;
            else  return mid;
        }
        return right;
    }
};

如果题目要求的时浮点数可以考虑利用浮点数二分搜索