NOIP2011pj表达式的值[树形DP 笛卡尔树

题目描述

对于1 位二进制变量定义两种运算：

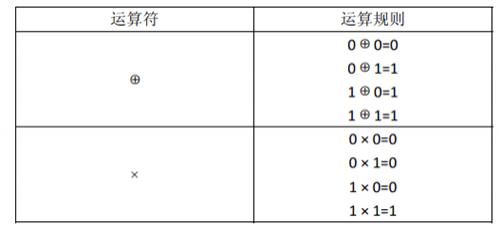
运算的优先级是：

先计算括号内的，再计算括号外的。
“× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如+(*_)，请你在横线处填入数字0 或者1 ，请问有多少种填法可以使得表达式的值为0 。

输入输出格式

输入格式：

输入文件名为exp.in ，共 2 行。

第1 行为一个整数 L，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含 L 个字符，其中只包含’（’、’）’、’+’、’*’这4 种字符，其中’（’、’）’是左右括号，’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号

输出格式：

输出文件exp.out 共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对10007 取模后的结果。

输入输出样例

输入样例#1：

4

+(*)

输出样例#1：

３

说明

【输入输出样例说明】

给定的表达式包括横线字符之后为：+(*_)

在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时，表达式的值均为0 ，所以共有3种填法。

【数据范围】

对于20% 的数据有 0 ≤ L ≤ 10。

对于50% 的数据有 0 ≤ L ≤ 1,000。

对于70% 的数据有 0 ≤ L ≤ 10,000 。

对于100%的数据有 0 ≤ L ≤ 100,000。

对于50% 的数据输入表达式中不含括号。

－－－－－－－－－－－－－－－－－－－－－－－－－

一开始想了一个区间DP的做法f[i][j][0/1]表示i到j为0或1的方案数，内存爆的连编译都不编译

然后想到建表达式树树形DP，白书上的方法只能拿80分

然后找到了这篇文章http://wenku.baidu.com/link?url=jvyUVTTGFC27LnlHkzQ0OObqeBFDwCYvuCbiHHG5CaPXrjFiGoBtiLhdfNIhW1vHNNZ-Umb_zTKnCOQK3WTw0N8KRQT8m2lfBBMsHpoIChC

用笛卡尔树建表达式树

百科

有点像treap，key按左右分，value按上下分

表达式树中key就是顺序，本来就按照这个顺序；value是算术优先级，设括号个数为p，'+':p*2+1 '*':p*2+2，value小的在上面

笛卡尔树有O(n)的建树方法：

可以发现key本来有序，新加的元素只能在当前的右链上，有可能吧本来右链上一些元素转到左子树上

用一个stack维护右链上的元素就好了，每次找第一个<=当前的

//

//  main.cpp

//  表达式的值树形dp

//

//  Created by Candy on 9/6/16.

//  Copyright ? 2016 Candy. All rights reserved.

//

#include <iostream>

#include <cstdio>

#include <algorithm>

#include <cstring>

#include <cmath>

using namespace std;

const int N=,MOD=;

int n;

char s[N];

struct node{

    int ls,rs;

    char op;

}tree[N*];

int cnt=,w[N],root=;

void build(){

    int p=,cnt=;

    for(int i=;i<=n;i++){

        if(s[i]=='(') p++;if(s[i]==')') p--;

        if(s[i]=='+') {w[++cnt]=p*+;

            tree[cnt].op=s[i];

        }

        if(s[i]=='*') w[++cnt]=p*+,tree[cnt].op=s[i];;

    }

    int st[N],k,top=-;

    for (int i=;i<=cnt;i++)

    {

        k = top;

        while (k >=  && w[st[k]] > w[i]) k--;

        if(k!=-) tree[st[k]].rs=i;

        if (k < top) tree[i].ls=st[k+];

        st[++k] = i;

        top=k;

    }

    root=st[];

}

int f[N][];

void dp(int i){//printf("dp %d\n",i);

    if(i==) return;

    if(f[i][]!=) return;

    int ls=tree[i].ls,rs=tree[i].rs;char op=tree[i].op;

    dp(ls);dp(rs);

    if(op=='+'){

        f[i][]=f[ls][]*f[rs][];

        f[i][]=f[ls][]*f[rs][]+f[ls][]*f[rs][]+f[ls][]*f[rs][];

    }

    if(op=='*'){

        f[i][]=f[ls][]*f[rs][];

        f[i][]=f[ls][]*f[rs][]+f[ls][]*f[rs][]+f[ls][]*f[rs][];

    }

    f[i][]%=MOD;f[i][]%=MOD;

}

int main(int argc, const char * argv[]) {

    scanf("%d%s",&n,s+);

    build();

    f[][]=f[][]=;

    dp(root);

    printf("%d",f[root][]%MOD);

    return ;

}

当然也可以用stack做，一个操作符栈一个数据栈，数据栈中是0/1的方案数

一开始push一个empty，以后每次一个+ *都push一个empty

//from 题解
//Candy?修改

#include<cstdio>

#include<cstring>

const int mod=;

struct node{

    int a,b;

}f[];

const node emp=(node){,};

char s[];

char st[];int n,tp=,fp=;

void cal(char op,node &a,node &b){

    if(op=='+') a.b=(a.b*(b.a+b.b)+a.a*b.b)%mod,a.a=a.a*b.a%mod;

    else a.a=(a.a*(b.a+b.b)+a.b*b.a)%mod,a.b=a.b*b.b%mod;

}

int main(){

    scanf("%d%s",&n,s);

    st[++tp]='('; f[++fp]=emp;

    s[n++]=')';

    for(int i=;i<n;i++){

        if(s[i]=='(')st[++tp]='(';

        else if(s[i]==')'){

            for(;st[tp]!='(';tp--,fp--)

                cal(st[tp],f[fp-],f[fp]);//pop 2 push 1

            tp--;// (

        }

        else{

            for(;st[tp]<=s[i]&&st[tp]!='(';tp--,fp--)// '*' < '+'

                cal(st[tp],f[fp-],f[fp]);

            st[++tp]=s[i],f[++fp]=emp;//every +/* with a number

        }

    }

    return!printf("%d\n",f[].a%mod);

}