paper 113：Bhattacharyya distance

在统计理论中，Bhattacharyya距离用来度量两个离散或连续概率分布的相似性。它与Bhattacharyya系数（Bhattacharyya coefficient）高度相关，后者是用来度量两个统计样本的重叠度的。所有这些命名都是为了纪念A. Bhattacharyya，一个在1930年工作于印度统计局的统计学家。该系数可以用来度量两个样本集的相似性。它通常在分类问题中被用来判断类别的可分性。

目录

·定义

·Bhattacharyya系数

定义

对于定义在同一个定义域X上的两个离散概率分布p和q来说，它们之间的Bhattacharyya距离可定义如下：

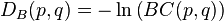
这里

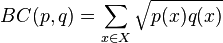
被称为Bhattacharyya系数。

对于连续概率分布，Bhattacharyya系数可以定义如下：

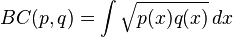
在以上两种情况下，0<=BC<=1并且0<=DB<=∞。DB并不遵循三角不等式，但是Hellinger距离满足三角不等式。

对于一个多维高斯分布来说pi=N(mi,Pi)，

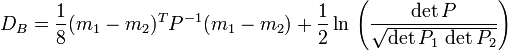
这里mi和Pi分别代表该分布的均值和方差，并且

注意到，在这种情况下Bhattacharyya距离的第一项类似于Mahalanobis距离（马氏距离）。

Bhattacharyya系数

Bhattacharyya系数用来度量两个统计样本的重叠度。该系数可以用来度量两个样本集的可分性。

计算Bhattacharyya系数包含了一个基本的关于两个样本集重合度的积分运算。两个样本集中的定义域被分成了事前定义的几份，这种划分可以体现在下面的定义中：

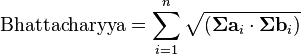
其中a，b代表样本，n代表划分的数目，∑ai和∑bi分别代表两个样本集中在第i个划分中的样本之和。

对于两个样本集来说，如果相同划分中的样本数越多，样本和越大，则该式的值越大。划分数的选择取决于每一个样本集中的样本数：太少的划分将因为过高估计了重叠区域而减小精度，而太多的划分将会因为在本该有重叠的区域没有恰好重叠而减小精度（最精细的划分将会使每一个相同的区间中都没有重叠）。

如果在每一个划分区间内的乘积都为零，则Bhattacharyya系数也为零。这就意味着如果A和B两个样本集都与样本集C完全可分，则BC（A，C）=B（B，C）=0，即Bhattacharyya系数对于A和B无法区分。

上述内容来自wikipedia

http://en.wikipedia.org/wiki/Bhattacharyya_distance