codeforces343A A. Rational Resistance

http://http://codeforces.com/problemset/problem/343/A

A. Rational Resistance

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.

However, all Mike has is lots of identical resistors with unit resistance
R₀ = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:

1. one resistor;
2. an element and one resistor plugged in sequence;
3. an element and one resistor plugged in parallel.

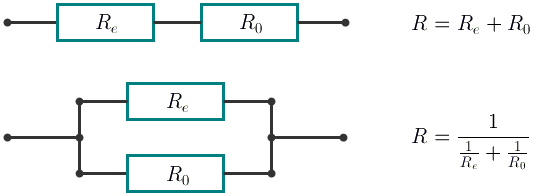
With the consecutive connection the resistance of the new element equals
R = R_e + R₀. With the parallel connection the resistance of the new element equals.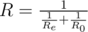
In this caseR_e equals the resistance of the element being connected.

Mike needs to assemble an element with a resistance equal to the fraction . Determine the smallest possible number of resistors
he needs to make such an element.

Input

The single input line contains two space-separated integers
a and b (1 ≤ a, b ≤ 10¹⁸). It is guaranteed that the fraction
is irreducible. It is guaranteed that a solution always exists.

Output

Print a single number — the answer to the problem.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use thecin,
cout streams or the%I64d specifier.

Sample test(s)

Input

1 1

Output

1

Input

3 2

Output

3

Input

199 200

Output

200

Note

In the first sample, one resistor is enough.

In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance.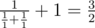
We cannot make this element using two resistors.

题目意思：有很多1欧姆的电阻，问最少用多少个电阻可以等效成a/b欧姆；

注意用__int64;

分析：这个题有个规律，就是a/b,b/a所需要的电阻一样，只是串并联关系不一样而已，因此该题可以这样考虑：写成假分子的形式a/b，（a>b）取整数部分，然后对剩余的电阻a1/b1进行类似的运算（a1>b1）

知道a/b可以除尽位置sum记录的整数值之和就是答案：

程序：

#include"string.h"
#include"stdio.h"
int main()
{
    __int64 a,b,p,t;
    while(scanf("%I64d%I64d",&a,&b)!=-1)
    {
        __int64 sum=0;
        while(1)
        {
            if(a<b)
            {
                t=a;
                a=b;
                b=t;
            }
            p=a/b;
            sum+=p;
            if(a%b==0)
                break;
            a-=b*p;
        }
        printf("%I64d\n",sum);
    }
}