Codeforces Round #360 (Div. 1) D. Dividing Kingdom II 并查集求奇偶元环

D. Dividing Kingdom II

 

Long time ago, there was a great kingdom and it was being ruled by The Great Arya and Pari The Great. These two had some problems about the numbers they like, so they decided to divide the great kingdom between themselves.

The great kingdom consisted of n cities numbered from 1 to n and m bidirectional roads between these cities, numbered from 1 to m. The i-th road had length equal to wi. The Great Arya and Pari The Great were discussing about destructing some prefix (all road with numbers less than some x) and suffix (all roads with numbers greater than some x) of the roads so there will remain only the roads with numbers l, l + 1, ..., r - 1 and r.

After that they will divide the great kingdom into two pieces (with each city belonging to exactly one piece) such that the hardness of the division is minimized. The hardness of a division is the maximum length of a road such that its both endpoints are in the same piece of the kingdom. In case there is no such road, the hardness of the division is considered to be equal to  - 1.

Historians found the map of the great kingdom, and they have q guesses about the l and r chosen by those great rulers. Given these data, for each guess li and ri print the minimum possible hardness of the division of the kingdom.

Input

 

The first line of the input contains three integers n, m and q (1 ≤ n, q ≤ 1000, 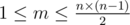) — the number of cities and roads in the great kingdom, and the number of guesses, respectively.

The i-th line of the following m lines contains three integers ui, vi and wi (1  ≤  ui,  vi  ≤  n, 0 ≤ wi ≤ 109), denoting the road number iconnects cities ui and vi and its length is equal wi. It's guaranteed that no road connects the city to itself and no pair of cities is connected by more than one road.

Each of the next q lines contains a pair of integers li and ri (1  ≤ li ≤ ri ≤ m) — a guess from the historians about the remaining roads in the kingdom.

Output

For each guess print the minimum possible hardness of the division in described scenario.

Example

input

5 6 5
5 4 86
5 1 0
1 3 38
2 1 33
2 4 28
2 3 40
3 5
2 6
1 3
2 3
1 6

output

-1
33
-1
-1
33

题意：
　　给你一个m边n点的无向有权图，q个询问，每次询问给你l,r求序号问l到r的边构成的图的hardness值
　　hardness值定义为：你可以任意选图中点划分为两点集合，取一个集合中任意相连两点的边权值的最大，取两个集合的max输出
　　当任意集合没有相连的两点为-1
题解：
　　画图.
　　奇元环必有一个非-1值
　　偶元环-1；
　　询问一次的话，按权值从大到小排序，按照并查集求奇偶环就好了
　　多次询问，q*m还是可以接受

　　

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int  N = 1e6+, inf = 2e9, mod = 1e9+;

int n,m,q,fa[N];
struct ss{int u,v,w,id;}p[N];
bool cmp(ss s1,ss s2){return s1.w>s2.w;}
void init(){for(int i=;i<=n*;i++)fa[i]=i;}
int finds(int x) {return x==fa[x]?x:fa[x]=finds(fa[x]);}

int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d%d",&p[i].u,&p[i].v,&p[i].w);
        p[i].id=i;
    }
    sort(p+,p+m+,cmp);
    while(q--)
    {
        int f=,l,r;
        scanf("%d%d",&l,&r);
        init();
        for(int i=;i<=m;i++)
        {
            if(p[i].id>=l&&p[i].id<=r)
            {
                int fx=finds(p[i].u),fy=finds(p[i].v);
                if(fx==fy)
                {
                    f=;
                    printf("%d\n",p[i].w);
                    break;
                }
                else
                {
                    fa[fx]=finds(p[i].v+n);
                    fa[fy)]=finds(p[i].u+n);
                }
            }
        }
       if(!f) printf("%d\n",-);
    }
    return ;
}