luogu2437 蜜蜂路线

题目大意

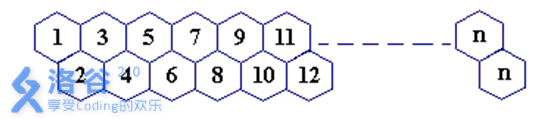
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房M开始爬到蜂房N，M<N，有多少种爬行路线？M,N<=1000

题解

看到M,N<=1000，我们不能寻求通项解。我们从动规的角度看，令f(i)为从1到达编号为i的蜂房爬行路线总数，则f(i)=f(i-1)+f(i-2)。这就是斐波那契数的定义呀！求f(n-m)即可。注意斐波那契数很大，要用到高精度。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAX_LEN = 1001, BASE = 10000, CARRY = 4;

struct BigInt
{
private:
	int A[MAX_LEN];
	int Len;

public:
	BigInt()
	{
		memset(A, 0, sizeof(A));
		Len = 0;
	}

	BigInt& operator += (const BigInt& a)
	{
		for (int i = 0; i <= max(Len, a.Len); i++)
		{
			A[i] += a.A[i];
			A[i + 1] += A[i] / BASE;
			A[i] %= BASE;
		}
		if (A[Len + 1])
			Len++;
		return *this;
	}

	BigInt& operator = (const BigInt& a)
	{
		memcpy(A, a.A, sizeof(A));
		Len = a.Len;
		return *this;
	}

	BigInt& operator = (int x)
	{
		memset(A, 0, sizeof(A));
		Len = 0;
		while (x)
		{
			A[Len++] = x%BASE;
			x /= BASE;
		}
		while (Len > 0 && A[Len] == 0)
			Len--;
		return *this;
	}

	BigInt operator +(const BigInt& a)
	{
		BigInt ans = *this;
		return ans += a;
	}

	void Print()
	{
		printf("%d", A[Len]);
		for (int i = Len - 1; i >= 0; i--)
			printf("%0*d", CARRY, A[i]);
	}
};

BigInt& GetF(int n)
{
	static BigInt F[3];
	F[0] = 1;
	F[1] = 1;
	for (int i = 2; i <= n; i++)
		F[i % 3] = F[(i - 1) % 3] + F[(i - 2) % 3];
	return F[n % 3];
}

int main()
{
	int n, m;
	scanf("%d%d", &m, &n);
	GetF(n - m).Print();
	return 0;
}