515Nod 1126 求递推序列的第n项【矩阵快速幂】

有一个序列是这样定义的：f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.

给出A，B和N，求f(n)的值。

Input

输入3个数：A,B,N。数字之间用空格分割。(-10000 <= A, B <= 10000, 1 <= N <= 10^9)

Output

输出f(n)的值。

Input示例

3 -1 5

Output示例

6

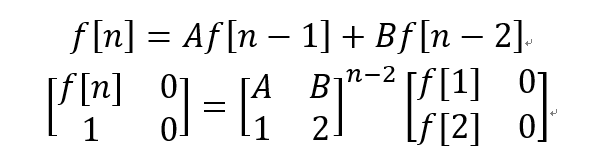
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
ll A,B,n;
struct matrix
{
    ll a[][];
};
matrix mutiply(matrix u,matrix v)
{
    matrix res;
    memset(res.a,,sizeof(res.a));
    for(int i=;i<;i++)
        for(int j=;j<;j++)
            for(int k=;k<;k++)
                res.a[i][j]=(res.a[i][j]+u.a[i][k]*v.a[k][j])%;
    return res;
}
matrix quick_pow(ll n)
{
    matrix ans,res;
    memset(res.a,,sizeof(res.a));
    for(int i=;i<;i++)
        res.a[i][i]=;
    ans.a[][]=A;ans.a[][]=B;
    ans.a[][]=;ans.a[][]=;
    while(n)
    {
        if(n&) res=mutiply(res,ans);
        n>>=;
        ans=mutiply(ans,ans);
    }
    return res;
}
int main()
{
    scanf("%lld%lld%lld",&A,&B,&n);
    if(n==) printf("1\n");
    else if(n==) printf("1\n");
    else
    {
        while(A<) A+=;
        while(B<) B+=;
        n-=;
        matrix ans=quick_pow(n);
        matrix res;
        res.a[][]=res.a[][]=;
        ans=mutiply(ans,res);
        printf("%lld\n",ans.a[][]);
    }
    return ;
}