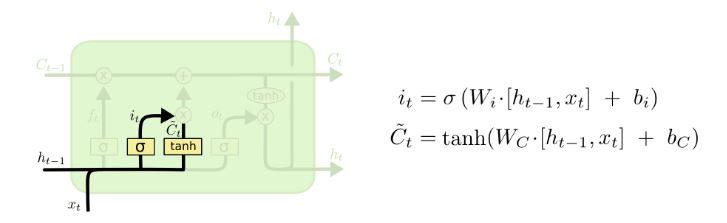机器学习:深入理解LSTM网络 (二)
之前我们介绍了RNN 网络结构以及其所遇到的问题,RNN 结构对于关联度太长的时序问题可能无法处理,
简单来说,RNN对于太久远的信息不能有效地储存,为了解决这个问题,有人提出了LSTM的网络结构,LSTM 网络结构最早是由 Hochreiter & Schmidhuber 在1997 年提出的,随着后来研究者的不断改进,LSTM网络在很多问题上都有非常好的表现,并且得到广泛的关注与应用。
LSTM 网络
LSTM 结构的一个优势在于可以很好的解决 “long-term dependency” 的问题,”长期记忆”是LSTM结构与生俱来的特性,而不需要刻意地去学习。
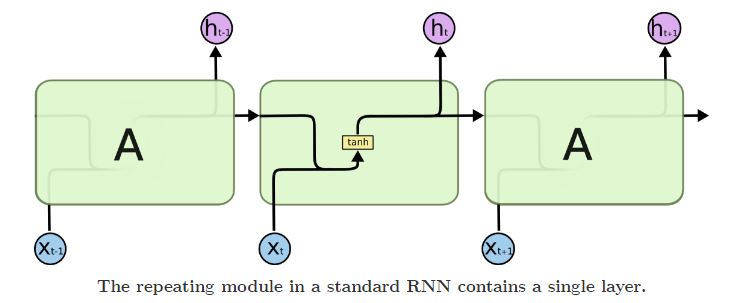
所有的RNN结构都是有一个不断重复的模块,在标准的RNN结构中,这个不断重复的模块是一个单层的tanh , 如下图所示:
表达式简单来说就是: ht=tanh(Wh⋅[ht−1,Xt]+bh)
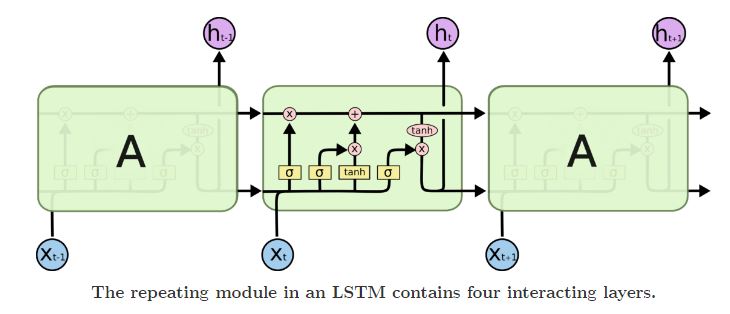
LSTM 网络也是有一个不断重复的模块,但是这个模块不是一个简单的tanh层,而是有复杂的四个网络层,用一种特殊的方式连接在一起,如下图所示:
LSTM 的核心思想
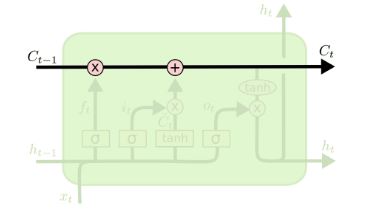
LSTM 网络的关键是 cell state,就是网络结构中最上面的那条水平线,如下图所示:
这条水平线贯穿整个网络,与一些线性组合相结合,可以将信息无改变的传递。
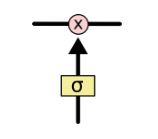
LSTM 网络具备的另外一种能力就是移除或者增加一些信息,这个过程是由一些称为传送门的结构来控制的,传送门可以让信息有选择的通过,这种门结构由sigmoid 层 与 点乘运算符组成。如下图所示:
其中,sigmoid 层输出 0-1 之间的数,控制信息传递的概率,1表示信息完全通过,0表示信息完全不能通过,一个典型的LSTM 网络有三个这样的传送门用来控制 cell state.
逐步深入LSTM
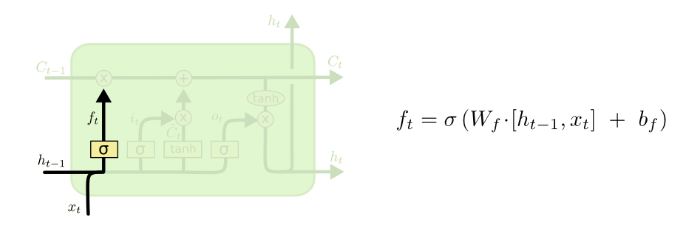
LSTM 网络的第一步就是决定哪些信息将从 cell state 中剔除掉,这一步是由一个sigmoid 层来负责的,sigmoid 层会根据输入的ht−1 和 xt输出一系列 0-1 之间的数,这些数表示了状态 Ct−1 中信息保存下来的概率,1 表示完全保存,而 0 表示完全剔除。结构及表达式如下图所示:
接下来的一步是要决定哪些新的信息需要存储在cell state 中,这一步有两部分,首先,一个称为 “input gate layer”的sigmoid 层会决定哪些信息要被更新,然后 一个 tanh 层会创建一个新的向量 C̃ t , 这个新的向量有可能被加入到 cell state 中,接下来的一步,我们会结合这两部分对cell state 创建一个更新,结构及表达式如下图所示:
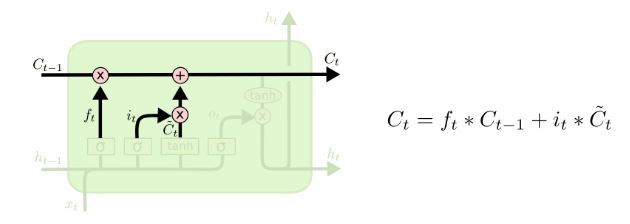
现在,就是对网络的旧状态Ct−1 进行更新到新的状态 Ct , 前面两部已经做好了所有的准备的工作,我们只需要进行简单的线性组合运算即可,结构及表达式如下图所示:
ft 和 it 是两个控制门,Ct−1 是网络的旧状态,C̃ t 是网络更新的信息,ft 表示有多少旧信息会被剔除,而 it 表示会有多少新的信息加入进来。
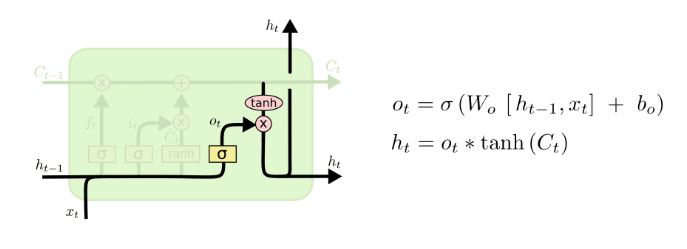
最后,我们需要给出输出,我们同样需要一个sigmoid层来决定Ct 中哪些是需要被输出的,然后我们让 cell state 通过一个 tanh 层 将值映射到到 [-1, 1]之间,然后乘以sigmoid层的输出,这样最终输出的就是我们决定输出的。结构与表达式如下图所示:
总得来说,LSTM结构,利用了几个传送门来控制信息的删除与更新,通过一些设计好的连接方式,可以拥有“长期记忆”的能力。与标准的RNN结构最大的区别就在于,LSTM是利用模块层里的神经网络来控制信息,而RNN是利用模块本身的连接方式来处理信息。所以与RNN相比,LSTM处理时序信息的能力要更强。性能也更稳定。
这里介绍的只是最常见的一种LSTM结构,实际上还有很多LSTM的变种,更加详细的介绍,可以参考colah 的博客。
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
机器学习:深入理解LSTM网络 (二)的更多相关文章
- (译)理解 LSTM 网络 (Understanding LSTM Networks by colah)
@翻译:huangyongye 原文链接: Understanding LSTM Networks 前言:其实之前就已经用过 LSTM 了,是在深度学习框架 keras 上直接用的,但是到现在对LST ...
- [转] 理解 LSTM 网络
[译] 理解 LSTM 网络 http://www.jianshu.com/p/9dc9f41f0b29 Recurrent Neural Networks 人类并不是每时每刻都从一片空白的大脑开始他 ...
- 【翻译】理解 LSTM 网络
目录 理解 LSTM 网络 递归神经网络 长期依赖性问题 LSTM 网络 LSTM 的核心想法 逐步解析 LSTM 的流程 长短期记忆的变种 结论 鸣谢 本文翻译自 Christopher Olah ...
- [译] 理解 LSTM 网络
原文链接:http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 吴恩达版:http://www.ai-start.com/dl2017/h ...
- 『cs231n』RNN之理解LSTM网络
概述 LSTM是RNN的增强版,1.RNN能完成的工作LSTM也都能胜任且有更好的效果:2.LSTM解决了RNN梯度消失或爆炸的问题,进而可以具有比RNN更为长时的记忆能力.LSTM网络比较复杂,而恰 ...
- 理解 LSTM 网络
递归神经网络 人类并不是每时每刻都从头开始思考.正如你阅读这篇文章的时候,你是在理解前面词语的基础上来理解每个词.你不会丢弃所有已知的信息而从头开始思考.你的思想具有持续性. 传统的神经网络不能做到这 ...
- Deep Learning基础--理解LSTM网络
循环神经网络(RNN) 人们的每次思考并不都是从零开始的.比如说你在阅读这篇文章时,你基于对前面的文字的理解来理解你目前阅读到的文字,而不是每读到一个文字时,都抛弃掉前面的思考,从头开始.你的记忆是有 ...
- 机器学习:深入理解 LSTM 网络 (一)
Recurrent Neural Network Long Short Term Memory Networks (LSTMs) 最近获得越来越多的关注,与传统的前向神经网络 (feedforward ...
- 理解LSTM网络--Understanding LSTM Networks(翻译一篇colah's blog)
colah的一篇讲解LSTM比较好的文章,翻译过来一起学习,原文地址:http://colah.github.io/posts/2015-08-Understanding-LSTMs/ ,Posted ...
随机推荐
- Eclipse下配置Ant脚本 自己主动打包带签名的Android apk
尽管eclipse非常少用了,可是在古老的项目上还是会用到.一个麻烦事是打带签名包的时候.非常不方便.下边纪录下配置ant,自己主动打包带签名apk的过程,作为备忘.(PC环境为MAC) 1,第一步得 ...
- Swift3.0为视图添加旋转动画_CABasicAnimation
Swift2.3: //创建旋转动画 let anim = CABasicAnimation(keyPath: "transform.rotation") //旋转角度 anim. ...
- Android事件分发机制具体解释
转载注明出处:http://blog.csdn.net/xiaohanluo/article/details/52416141 1. 概述 Android日常研发时,与View接触占领相当多的时间.而 ...
- sublim课程2 sublim编辑器的使用(敲代码的时候把这个放旁边用)
sublim课程2 sublim编辑器的使用(敲代码的时候把这个放旁边用) 一.总结 一句话总结:不必一次记住所有,不可能也得不偿失,先记住常用,慢慢来.(敲代码的时候把这个放旁边用,一下子就熟了 ...
- linux中竖线'|',双竖线‘||’,&和&&的意思
对于初学者来说这几个意思可能只知道其中几个的意思,下面我们来看一下. 1.竖线'|' ,在linux中是作为管道符的,将'|'前面命令的输出作为'|'后面的输入.举个例子 [18066609@root ...
- Java设计模式之从[暗黑破坏神存档点]分析备忘录(Memento)模式
在大部分游戏中,都有一个"存档点"的概念.比如,在挑战boss前,游戏会在某个地方存档,假设玩家挑战boss失败,则会从这个存档点開始又一次游戏.因此,我们能够将这个"存 ...
- 忙里偷闲( ˇˍˇ )闲里偷学【C语言篇】——(7)结构体
一.为什么需要结构体? 为了表示一些复杂的事物,而普通类型无法满足实际需求 二.什么叫结构体? 把一些基本类型组合在一起形成的一个新的复合数据类型叫做结构体. 三.如何定义一个结构体? 第一种方式: ...
- 微信小程序从零开始开发步骤(三)
上一章节,我们分享了如何创建一个新的页面和设置页面的标题,这一章我们来聊聊底部导航栏是如何实现的.即点击底部的导航,会实现不同对应页面之间的切换. 我们先来看个我们要实现的底部导航栏的效果图:(三个导 ...
- 具体分析contrex-A9的汇编代码__switch_to(进程切换)
//函数原型:版本号linux-3.0.8 struct task_struct *__switch_to(structtask_struct *, struct thread_info *, str ...
- 数据预处理(normalize、scale)
matlab 工具函数(三)-- normalize(归一化数据) 注:待处理的数据 X∈Rd×N,N 表示样本的个数,d 则是单个样本的维度: 1. 去均值(remove DC) X = bsxfu ...