极化码的matlab仿真(2)——编码

第二篇我们来介绍一下极化码的编码。

首先为了方便进行编码，我们需要进行数组的定义

signal = randi([0,1],1,ST);       %信息位比特，随机二进制数
frozen = zeros(1,FT);             %固定位比特，规定全为0
encode = zeros(1,N * block);      %编码后的比特
noise = snr(i) ^ 1/2 * randn(1,N * block);  %加性高斯白噪声

极化码的编码重点在于生成矩阵的产生，以及信息位、冻结位的选取。

• 我们先来看生成矩阵的产生。

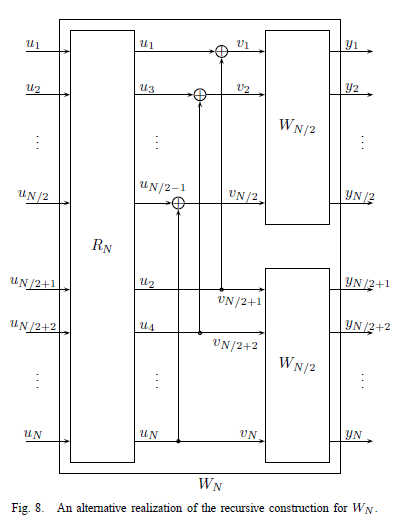
这是Arikan论文中的编码示意图，好像挺复杂，不过看不懂也没关系。我们来看一下编码过程中都做了哪些事。

首先是向量元素的翻转，通过翻转矩阵R_N来实现，然后是信道的联合和信道的分裂。

什么？你问我为什么要这样做？我也不知道，极化码本身就建立在信道极化的现象之上，信道极化就是信道以特定方式联合和分裂所产生的现象。要想问为什么这么做，到土耳其找Arikan教授喝茶去吧。

论文中将这个翻转过程简化为矩阵运算，这就为我们进行程序仿真提供了方便：

其中：

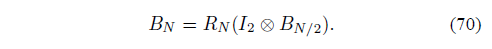
B_N 为排序矩阵，以N=8为例，解释它的作用：

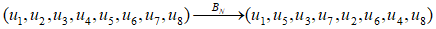
传化过程为：%将向量下标减一后，转化为二进制数%----%将得到的二进制数反序排列%----%将反序后的二进制数转化为十进制数，加一%

例：

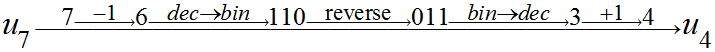
我们通过 B_N 的递推式可以求得 B_N，再将其与 F 的 n 次克劳尼克积相乘，就能够得到生成矩阵。

这样说你明白了吗？什么？没有？？？

不错，说明你是个正常人。实际编码的时候，如果真的在matlab中将上述过程模拟一遍来求生成矩阵的话，是非常耗时耗力的。我们还有另外一条路可以走——找规律。

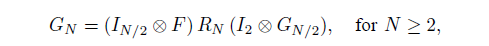
上式为 G_N 的原始求解方法，其中 I 为单位矩阵，F 定义为[1 0; 1 1]，R_N 为翻转矩阵，对于 ，有：

N=4：

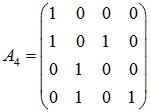
N=8：

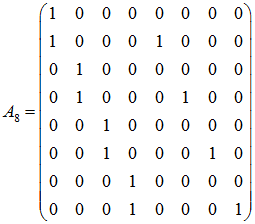
可以发现 A 的元素排列十分有规律。前 N/2 列元素总是奇偶成对出现“1”，后 N/2 元素仅出现在偶数位，且与同处在一行的前一个“1”保持固定距离。根据此规律编写程序如下：

for i = 1 : N/2
    A(2 * i - 1, i) = 1;
    A(2 * i, i) = 1;
    A(2 * i, N / 2 + i) = 1;
end

递归部分：

G = A * kron(eye(2),Gpre);    %Gpre即上一层递归所得生成矩阵
Gpre = G;

如果将生成矩阵的产生编写为一个函数，则代码如下：

function GN = G(n)
    N = 2 ^ n;
    Gpre = 1;
    for i=1:n　　　　　　　%每一层递归都相当于计算一个新的生成矩阵
        Ni = 2 ^ i;　　　　%这个新的生成矩阵的维度为 Ni/2
        G = zeros(Ni);
        %Fn = zeros(Ni);
        A = zeros(Ni);
        for j = 1 : Ni / 2
            A(2 * j - 1 , j) = 1;
            A(2 * j , j) = 1;
            A(2 * j , Ni / 2 + j) = 1;
        end
        G = A*kron(eye(2),Gpre);
        Gpre = G;
    end
    GN = G;
end

• 其次，来看信息位与冻结位的选取

信道极化过程中，有一部分信道的信道容量 I(W) 可以到达1，另一部分则趋近于0。信道容量反映了信道无失真传输的最大信息率，我们可以通过计算联合、分裂后各信道的信道容量并对它们进行排序，然后根据码率，选择排序靠前的信道作为信息传输的信道，剩余的信道用来传输冻结位。

另一种方法是计算巴氏参数Z(W)，对于一个给定信道，巴氏参数越大说明该信道越不可靠。因此我们只需计算出联合、分裂后信道的巴氏参数，并对它们进行排序，然后根据码率选择巴氏参数较小的信道作为信息位，剩余信道作为冻结位。Arikan论文中给出了巴氏参数的递归求解办法，这使得我们能够很方便的通过matlab实现信息位的选取。

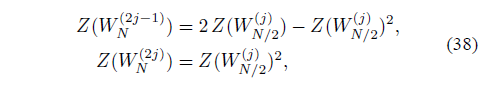
% 将巴氏参数计算过程封装在函数B_para之中方便调用，Z为数组，作为实参传递进来。数组中只有第一个元素。
% Z第一个元素可以通过计算得到，计算公式为Z(1) = 2*(p*(1-p))^0.5;
function y = B_para(Z)
for i = 1 : log2(N)         %迭代次数，N为码长
    Z_pre = Z;              %z_pre为上一层信道巴氏参数
    for j = 1 : 2^(i-1)     %本层运算使用的下标
        Z(2*j-1) = 2*Z_pre(j) - Z_pre(j)^2;
        Z(2*j) = Z_pre(j)^2;    %递推公式
    end
end　　
y = z;　　　　% y作为实参从函数中传递出去，y就是最终的巴氏参数

得到巴氏参数序列后，下面的操作就是将此序列进行排序，并根据码率确定信息位和固定位。

[Z_in_order,index] = sort( y );            %将巴氏参数从小到大排列
signal_index = sort( index( 1:S ) );    　　%前S位作为信息位
frozen_index = sort( index( s+1:end ) );    %后面的作为冻结位

得到了生成矩阵，确定了信息位冻结位，下面要做的就是进行编码。

for j=1:block　　　　%对每一个码块都要进行编码处理
    encoded(1,((j-1)*N+1):(j*N)) = signal(((j-1)*S+1):(j*S))*G(signal_index,:) + frozen(((j-1)*F+1):(j*F))*G(frozen_index,:);
end　　　　　　　　　　　　　　　　　　%进行编码
encode = mod(encode,2);		　%对2取模
encode = 2 * encode - 1;　　　　   %符号化
encode = encode + noise;	  %叠加噪声

数组 encode 就是我们得到的编码矩阵。

编码matlab实现就是这样，为了照顾和知识点讲解同步，各个部分代码并未进行完整、严谨的书写。本系列最后我会整合与各章节中分散的代码，为大家带来可运行的代码，并将M文件附在文后。敬请期待。

下一节我们要探讨的是polar code中非常重要的译码部分——连续消除译码（SC译码）。