[杂题]HDOJ5515 Game of Flying Circus

嗯。。。这是一道水题。。。

鉴于还没人写这题的题解， 那我就来写一发。

题意：有个边长为300米的正方形

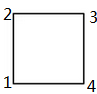嗯  这样标号

有两个人A和S，开始的时候A、S都在1(左下角)那个位置。

两个人都要按照2、3、4、1的顺序走。

有两个得分的方法：  ①. 比对手先走到点(2或3或4或1) 先走到的得1分，后走到的不得分。

②. A把S打一顿，A得一分。

题目问的是A能不能获得胜利。

A在正方形里面也是可以随便走的。(比如A能直接从1走直线到3， 但是如果他要得分，他必须回到2，按照2341的顺序走 才能得分)

A只能打S一次，打完之后S会昏迷T秒。A不能在  S到2号点  之前打晕他。

题目保证A的速度$v_1$小于等于S的速度$v_2$。

若是A、S同时到达 点 上，那么是A或B先得分，A再打人的。如果两个人都能得分，那A先得分

分析：

A比S慢，所以肯定要尽早把S打昏了，才能开始得分。

因为A也要按照2341的顺序走，所以打晕S的位置应尽量靠近2(这样重复走的路才少)

因为总共有5分(2、3、4、1四个点四分，A打S 一分)，所以A要至少获得3分才能获胜，也就是至少得到2个点的分。

总体可以分为  在2、3之间把S打晕  和  在3、4之间把S打晕  两种情况。

(1、4之间打晕明显是不行的。因为S已经通过2、3、4走到1、4之间了， 那么S就已经得到了3分，A已经不可能获胜了)

特别的，考虑一下4号点。

若A选择在4号点打晕S，那么A是从1走过来的，此时A不能得分。(根据题目 先得分 再打人 )那么S就先得到4号点的分数，A之后才打晕S，

故4号点打晕S也是不能获胜的。

在2、3或者3、4打晕S的情况，(如上分析 要尽量靠近2号点，所以)应在恰好相遇的地方打晕S，而不存在 到达某地 等着S过来打晕他的情况。

那就只要解出相遇的位置，

在2、3打晕S的  判断下A能否先到(或者同时)到4号点

在3、4打晕S的  判断下A能否先到(或者同时)到1号点

Ⅰ.

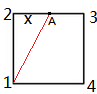
设相遇点为A 2到A的距离为x

$\frac{\sqrt{x^2+300^2}}{v_1}=\frac{300+x}{v_2}$   解出$x$

判断A(回2)到3、4的时间是否小于等于S昏迷之后到4的时间即可。

Ⅱ.

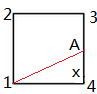
$\frac{\sqrt{x^2+300^2}}{v_1}=\frac{900-x}{v_2}$   解出$x$

判断A(回2)到3、4、1的时间是否小于等于S昏迷之后到1的时间即可。

这种情况A回2号点肯定是走的直线，不必经过3号点。

用求根公式的时候注意正负的取舍(因为是单调的，所以不可能两个根都合法)

(分母为$v_1^2-v_2^2$) 注意分母为零，也就是$v_1=v_2$的时候 特判一下。

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 typedef pair<int, int> PI;
 const int N=1e5;
 const double eps=1e-;
 const LL mod=1e9+;

 int main()
 {
     int t, ca=;
     scanf("%d", &t);
     while(t--)
     {
         double t, v1, v2;
         scanf("%lf%lf%lf", &t, &v1, &v2);
         printf("Case #%d: ", ca++);
         if(v1==v2)
         {
             puts("Yes");
             continue;
         }
         double tt1=*sqrt(2.0)/v1;  // a dao 3
         double tt2=600.0/v2;          // b dao 3
         double v12=v1*v1, v22=v2*v2;
         double t1=300.0/v1;  // a dao 4
         double t2=900.0/v2;  // b dao 4
         if(t1>=t2)
         {
             puts("No");
             continue;
         }
         if(tt1<=tt2)  // zai 2 3
         {
             double dt=(*v12)*(*v12)-*(v12-v22)*(v12*-*v22);
             double x=(-600.0*v12+sqrt(dt))/2.0/(v12-v22);
             if((x+)/v1<=t+(-x)/v2)
             {
                 puts("Yes");
                 continue;
             }
         }
         // zai 3 4

             double dt=(*v12)*(*v12)-*(v12-v22)*(v12*-*v22);
             double x=(1800.0*v12-sqrt(dt))/2.0/(v12-v22);
             if(sqrt((300.0-x)*(300.0-x)+90000.0)/v1+900.0/v1<=t+(+x)/v2)
                 puts("Yes");
             else
                 puts("No");

     }
     return ;
 }

HDOJ5515

这题题目比较长，所以大家都没看吧。。。

重现抢了个FB 哈哈