P5018 对称二叉树题解

题目内容链接：

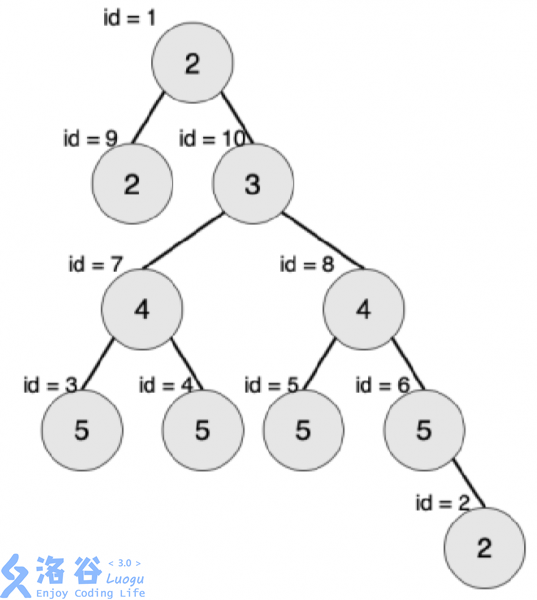
那么根据题意，上图不是对称二叉树，只有节点7的子树是；

通俗来说，对称二叉树就是已一个节点x为根的子树有穿过x点的对称轴并且对称轴两边的对称点的大小也必须相等，那么这棵树就是对称二叉树。

思路也很简单：递归处理每个节点的子树的节点数size，然后枚举每一个节点的子树来判断是否为对称二叉树。如果一边有节点另一边没有就return剪枝，一旦碰到不一样的节点就剪枝。

特别的，单个节点也是一个对称二叉树。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
using namespace std;
int read(){//快读
    int k = , f = ; char c = getchar();
    while(c < '' || c > ''){
        if(c == '-') f = -;
        c = getchar();
    }
    while(c >= '' && c <= ''){
        k = k *  + c - ; c = getchar();
    }
    return k * f;
}
int val[], size[], ans;
struct zzz {
    int l, r;
}node[];
int dfs(int pos) {//
    if(pos == -) return ;
    size[pos] = dfs(node[pos].l) + dfs(node[pos].r) + ;
    return size[pos];
}
bool duichen(int ls, int rs) {//判断对称
    if(ls == rs && ls == -) return ;
    if(val[ls] == val[rs] && size[ls] == size[rs] && duichen(node[ls].l, node[rs].r) && duichen(node[ls].r, node[rs].l))
        return ;
    return ;
}
int main(){
    int n = read();
    for(int i = ; i <= n; ++i) val[i]=read();
    for(int i = ; i <= n; ++i)
      node[i].l = read(), node[i].r = read();
    dfs();
    for(int i = ; i <= n; ++i)
        if(duichen(node[i].l, node[i].r)) ans = max(ans, size[i]);
    printf("%d\n", ans);
    return ;
}

完结