牛客练习赛26B 烟花 （概率DP）

链接：https://ac.nowcoder.com/acm/contest/180/B

来源：牛客网

烟花

时间限制：C/C++ 1秒，其他语言2秒

空间限制：C/C++ 262144K，其他语言524288K

Special Judge, 64bit IO Format: %lld

题目描述

小a有nn个烟花，每个烟花代表着互不相同的颜色，对于第ii个烟花，它有p_ip

i

​

的概率点燃，现在小a要去点燃它们，他想知道产生颜色的期望个数 及 产生恰好产生kk种颜色的概率

输入描述:

第一行两个整数n,kn,k

接下来一行nn个数，第ii个数p_ip

i

​

表示第ii个烟花被点燃的概率

输出描述:

输出有两行

第一行表示产生不同颜色的期望个数

第二行表示产生恰好kk种颜色的概率

以换行符分割

示例1

输入

复制

3 2

0.5 0.25 0.75

输出

复制

1.5000

0.4062

说明

第二问样例解释：

(1, 2) :0.5 * 0.25 * (1 - 0.75) = 0.03125(1,2):0.5∗0.25∗(1−0.75)=0.03125

(1, 3): 0.5 * (1 - 0.25) * 0.75 = 0.28125(1,3):0.5∗(1−0.25)∗0.75=0.28125

(2, 3) :(1 - 0.5) * 0.25 * 0.75 = 0.09375(2,3):(1−0.5)∗0.25∗0.75=0.09375

相加得0.406250.40625

备注:

对于30 %30%的数据：n \leqslant 6, k \leqslant nn⩽6,k⩽n

对于100 %100%的数据：n \leqslant 10^5, k \leqslant 2 * 10^2n⩽10

5

,k⩽2∗10

2

输出均保留4位小数,若你的答案误差与std不超过10^{-4}10

−4

即为正确

题意：



思路：

因为每一个烟花对颜色个数的贡献是1 所以

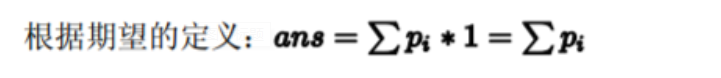
第2个输出用概率dp来做，

定义dp状态 dp[i][j] 到第i个烟花是，已经燃放了j个烟花的概率。。

对于每一个烟花只有两个状态，点燃和不点燃，所以

当前 dp[i][j] = dp[i-1][j-1]a[i]+ dp[i-1][j](1.0000-a[i]) 即i-1个烟花只点燃了j-1个烟花的时，我在用a[i] 的概率去点燃当前第i个烟花，那么就是第i个烟花时点燃了 j 个烟花，

还有一个 就是 i个烟花时，就点燃了j个烟花，当前的烟花不点燃，就是第i个烟花时点燃了 j 个烟花， 加起来就是dp[i][j]

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll powmod(ll a,ll b,ll MOD){ll ans=1;while(b){if(b%2)ans=ans*a%MOD;a=a*a%MOD;b/=2;}return ans;}
inline void getInt(int* p);
const int maxn=100010;
const int inf=0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
double a[maxn];
double dp[maxn][202];
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    gbtb;
    cin>>n;
    cin>>k;
    repd(i,1,n)
    {
        cin>>a[i];
    }
    repd(i,1,n)
    {
        repd(j,1,i)
        {
            dp[i][j]+=dp[i-1][j-1]*a[i];
            dp[i][j]+=dp[i-1][j]*(1.0000-a[i]);
        }
    }
    cout<<fixed<<setprecison()

    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}