opencv的曲线拟合polyfit

4.1 曲线拟合的最小二乘法

求以下拟合函数

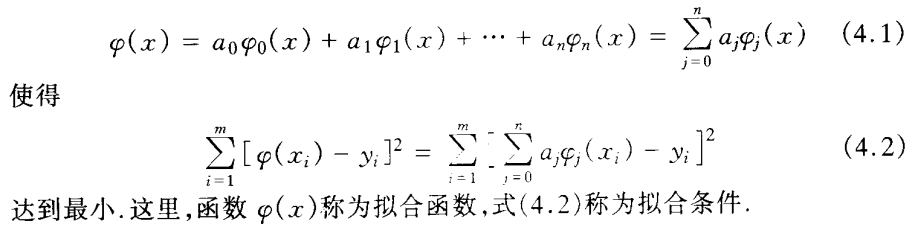
拟合条件：拟合曲线与各数据点在y方向的误差平方和最小.

拟合函数为一元函数时--函数图形为平面曲线--曲线拟合

解决曲线拟合，最先是确定拟合函数的形式。即适当选取

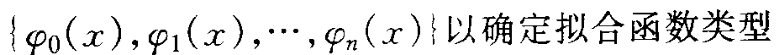
选幂函数{1,x,x², ···,xⁿ}, 则多项式拟合函数φ(x)可表示为：

φ(x)=a₀+a₁*x+a₂*x²+a₃*x³+......+an*xⁿ =[a₀ a₁ a₂ ...... a_n][1 x₁ x₁² ... ... x₁ⁿ]^T (n+1<m)

a0、a1、a2......an是幂系数，也是拟合所求的未知量。

实际中拟合函数有指数函数、三角函数等，根据数据的分布特点来选取合适的拟合函数。

将第 i 个样本点的x坐标带入φ(x)，得到：

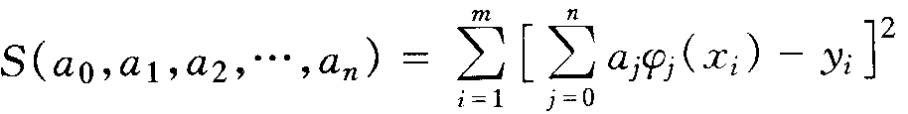
这个就是二次方程，我们期望S最小。此时，方程中的x、y已知，想求的是a₀ a₁ a₂ ...... a_n。

S最小的必要条件是：

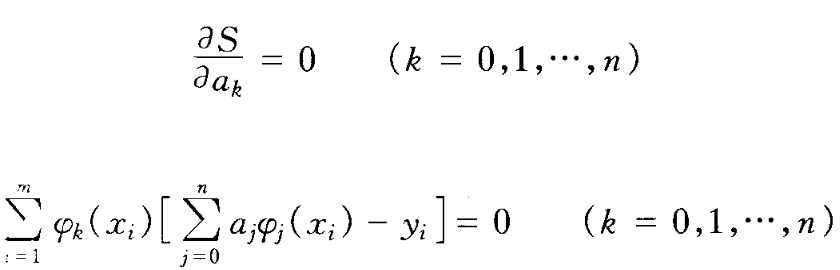
整理得到如下正规方程组：

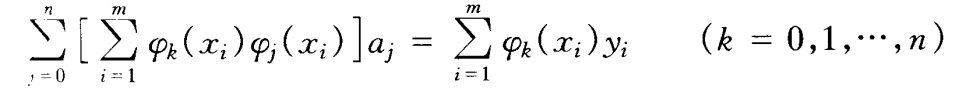
解此方程组得系数a₀ a₁ a₂ ...... a_n，, 得出拟合函数φ(x)

最小二乘法：以残差平方和最小问题的解来确定拟合函数

二、超定方程组得最小二乘解

将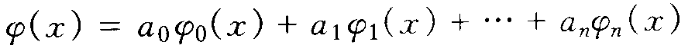

写成向量内积形式：

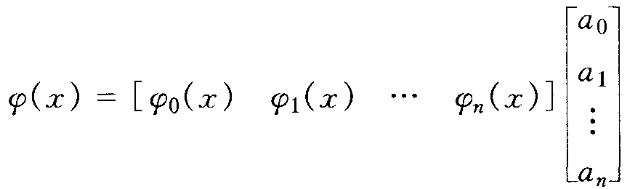
a₀ a₁ a₂ ...... a_n为待定系数，满足：

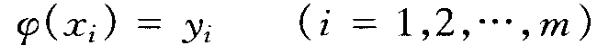
此m个等式如下建立方程组：

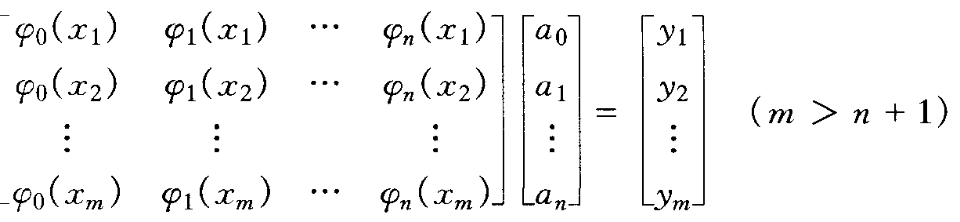
方程数(m)多于未知数个数(n+1)，此类方程组称为超定方程组。下列正规方程组中k个方程中a_j的系数

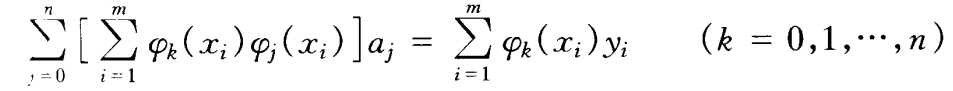
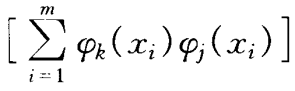
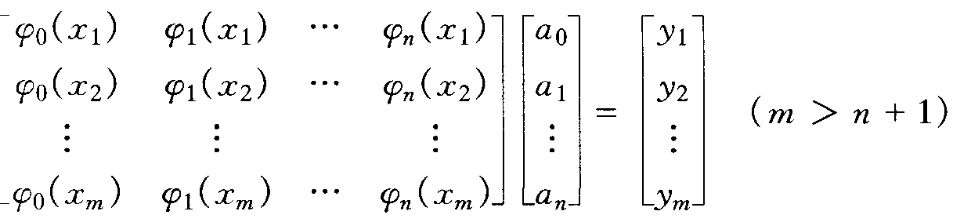
经推导，得到最小二次方，幂函数拟合公式如下：

Φ^T* Φ*a= Φ^T*y

其中Φ是样本点坐标x的超定矩阵，将所有x带入该向量[1 x x^2 ... ... x^n]中，就得到超定矩阵Φ。Φ^T表示Φ的转置

#include <iostream>

#include<opencv2/opencv.hpp>

using namespace std;

using namespace cv;

//下面宏定义CV_MAT_ELEM2为方便快速访问图像像素

#define CV_MAT_ELEM2(src,dtype,y,x) \

        (dtype*)(src.data+src.step[]*y+src.step[]*x)

Mat polyfit(std::vector<cv::Point2f> &chain,int n)

{

    Mat y(chain.size(),,CV_32F,Scalar::all());

/* ********【预声明phy超定矩阵】************************/

/* 多项式拟合的函数为多项幂函数

 * f(x)=a0+a1*x+a2*x^2+a3*x^3+......+an*x^n

 *a0、a1、a2......an是幂系数，也是拟合所求的未知量。设有m个抽样点，则：

 * 超定矩阵phy=1 x1 x1^2 ... ...  x1^n

 *           1 x2 x2^2 ... ...  x2^n

 *           1 x3 x3^2 ... ...  x3^n

 *              ... ... ... ...

 *              ... ... ... ...

 *           1 xm xm^2 ... ...  xm^n

 *

 * *************************************************/

    cv::Mat phy(chain.size(),n,CV_32F,Scalar::all());

    for(int i=;i<phy.rows;i++)

    {

        float* pr=phy.ptr<float>(i);

        for(int j=;j<phy.cols;j++)

        {

           pr[j]=pow(chain[i].x,j);

        }

        y.at<float>(i)=chain[i].y;

    }

    Mat phy_t=phy.t();

    Mat phyMULphy_t=phy.t()*phy;

    Mat phyMphyInv=phyMULphy_t.inv();

    Mat a=phyMphyInv*phy_t;

    a=a*y;

    return a;

}

int main()

{

    vector<Point2f> sp;

    //设有二次曲线点 g(x)=5+2.6x+2x^3,则:

    float a[]={,2.6,};

    Mat image(,,CV_32FC1,Scalar());

    RNG rng;//预声明一个随机变量，用于作为离散点的干扰项

    for(int i=;i<;i+=)

    {

        Point2f p;

        p.x=i;

        for(int k=;k<sizeof(a);k++)

        {

            p.y +=a[k]*pow(i,k);//

        }

        p.y +=rng.uniform(-,);//为理想点位置添加随机干扰

     /*将上面的p点以圆点的形式绘制到image上，为了观察方便，

      * 将y坐标做了颠倒，坐标原点在image的左下角*/

        Point2f pi;

        pi.x=p.x;

        pi.y=image.rows-p.y;

        circle(image,pi,,Scalar(),-);

      /*-------------end--------------------*/

        sp.push_back(p);

        cout<<p<<endl;

    }

    image.convertTo(image,CV_8UC1);

    imshow("distributed Points",image);

    Mat am=polyfit(sp,);

    cout<<am<<endl;

    waitKey();

    return ;

}