2021-11-27：给定一个数组arr，长度为N，做出一个结构，可以高效的做如下的查询: 1) int querySum(L,R) : 查询arr[L...R]上的累加和； 2) int query

2021-11-27：给定一个数组arr，长度为N，做出一个结构，可以高效的做如下的查询:

1. int querySum(L,R) : 查询arr[L…R]上的累加和;
2. int queryAim(L,R) : 查询arr[L…R]上的目标值，目标值定义如下：
   假设arr[L…R]上的值为[a,b,c,d]，a+b+c+d = s,
   目标值为 : (s-a)^2 + (s-b)^2 + (s-c)^2 + (s-d)^2;
3. int queryMax(L,R) : 查询arr[L…R]上的最大值.
   要求：
4. 初始化该结构的时间复杂度不能超过O(N*logN)；
5. 三个查询的时间复杂度不能超过O(logN)；
6. 查询时，认为arr的下标从1开始，比如 :
   arr = [ 1, 1, 2, 3 ];
   querySum(1, 3) -> 4;
   queryAim(2, 4) -> 50;
   queryMax(1, 4) -> 3。
   来自美团。

答案2021-11-27：

querySum方法，前缀和。
queryAim方法，前缀和，平方数组的前缀和，线段树。对目标值展开，(N-2)*S平方+a1的平方+a2的平方+…+an的平方。
queryMax方法，线段树。

代码用golang编写。代码如下：

package main

import (
    "fmt"
    "math"
)

func main() {
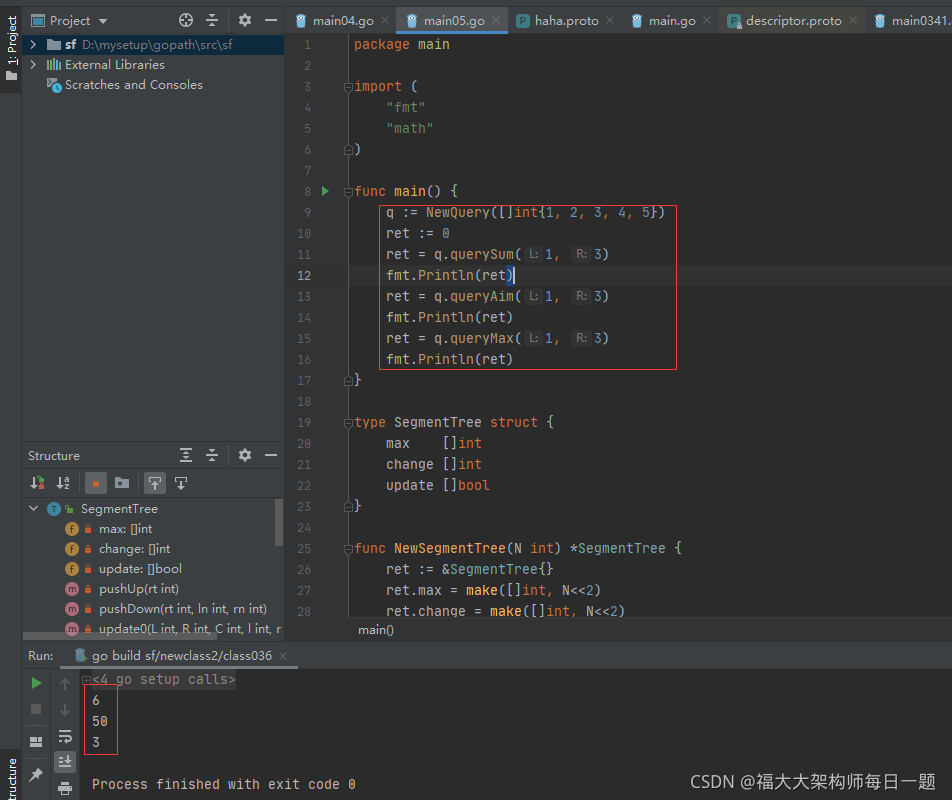
    q := NewQuery([]int{1, 2, 3, 4, 5})
    ret := 0
    ret = q.querySum(1, 3)
    fmt.Println(ret)
    ret = q.queryAim(1, 3)
    fmt.Println(ret)
    ret = q.queryMax(1, 3)
    fmt.Println(ret)
}

type SegmentTree struct {
    max    []int
    change []int
    update []bool
}

func NewSegmentTree(N int) *SegmentTree {
    ret := &SegmentTree{}
    ret.max = make([]int, N<<2)
    ret.change = make([]int, N<<2)
    ret.update = make([]bool, N<<2)
    for i := 0; i < len(ret.max); i++ {
        ret.max[i] = math.MinInt64
        return ret
    }
    return ret
}

func (this *SegmentTree) pushUp(rt int) {
    this.max[rt] = getMax(this.max[rt<<1], this.max[rt<<1|1])
}

func getMax(a int, b int) int {
    if a > b {
        return a
    } else {
        return b
    }
}

// ln表示左子树元素结点个数，rn表示右子树结点个数
func (this *SegmentTree) pushDown(rt, ln, rn int) {
    if this.update[rt] {
        this.update[rt<<1] = true
        this.update[rt<<1|1] = true
        this.change[rt<<1] = this.change[rt]
        this.change[rt<<1|1] = this.change[rt]
        this.max[rt<<1] = this.change[rt]
        this.max[rt<<1|1] = this.change[rt]
        this.update[rt] = false
    }
}

func (this *SegmentTree) update0(L, R, C, l, r, rt int) {
    if L <= l && r <= R {
        this.update[rt] = true
        this.change[rt] = C
        this.max[rt] = C
        return
    }
    mid := (l + r) >> 1
    this.pushDown(rt, mid-l+1, r-mid)
    if L <= mid {
        this.update0(L, R, C, l, mid, rt<<1)
    }
    if R > mid {
        this.update0(L, R, C, mid+1, r, rt<<1|1)
    }
    this.pushUp(rt)
}

func (this *SegmentTree) query(L, R, l, r, rt int) int {
    if L <= l && r <= R {
        return this.max[rt]
    }
    mid := (l + r) >> 1
    this.pushDown(rt, mid-l+1, r-mid)
    left := 0
    right := 0
    if L <= mid {
        left = this.query(L, R, l, mid, rt<<1)
    }
    if R > mid {
        right = this.query(L, R, mid+1, r, rt<<1|1)
    }
    return getMax(left, right)
}

type Query struct {
    sum1 []int
    sum2 []int
    st   *SegmentTree
    m    int
}

func NewQuery(arr []int) *Query {
    ret := &Query{}
    n := len(arr)
    ret.m = len(arr) + 1
    ret.sum1 = make([]int, ret.m)
    ret.sum2 = make([]int, ret.m)
    ret.st = NewSegmentTree(ret.m)
    for i := 0; i < n; i++ {
        ret.sum1[i+1] = ret.sum1[i] + arr[i]
        ret.sum2[i+1] = ret.sum2[i] + arr[i]*arr[i]
        ret.st.update0(i+1, i+1, arr[i], 1, ret.m, 1)
    }
    return ret
}

func (this *Query) querySum(L, R int) int {
    return this.sum1[R] - this.sum1[L-1]
}

func (this *Query) queryAim(L, R int) int {
    sumPower2 := this.querySum(L, R)
    sumPower2 *= sumPower2
    return this.sum2[R] - this.sum2[L-1] + (R-L-1)*sumPower2
}

func (this *Query) queryMax(L, R int) int {
    return this.st.query(L, R, 1, this.m, 1)
}

执行结果如下：

---

左神java代码