#分治#JZOJ 4211 送你一颗圣诞树

题目

有\(m+1\)棵树分别为\(T_{0\sim m}\)，一开始只有\(T_0\)有一个点，编号为0。

对于每棵树\(T_i\)由T_{a_i}\(的第\)c_i\(个点与\)T_{b_i}\(的第\)d_i\(个点连接后形成。
其中边\)(c_i,d_i)\(的权值为\)l_i\(，若\)T_{a_i}\(有\)s\(个节点，那么原\)T_{b_i}\(部分的编号都要加上\)s\(
问对于任意一棵树，求任意两点间的距离之和。(\)m\leq 60$)

---

分析

首先\(ans_{T_i}=ans_{T_{a_i}}+ans_{T_{b_i}}+l_i*siz_{T_{a_i}}*siz_{T_{b_i}}+两个子树到其根节点的距离之和\)

前面三个都很好处理，第四个考虑分治，然后用map记忆化答案，保证记录的两个点在同一棵树内

（\(x<y\)表示\(x\)到\(y\)的距离，\(y=0\)表示各点到点\(x\)的距离之和）

首先两点间距离很好求，不同子树内拆开两部分合并，同子树内跳到子树内

然后各点到根节点（选择合并的点）的距离



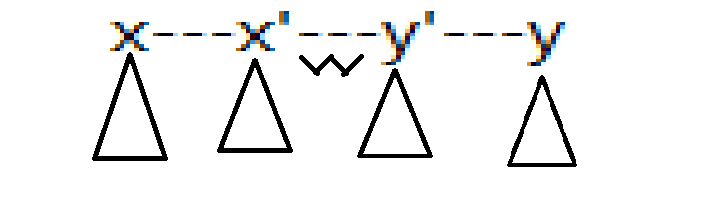
如果\(x\)在左子树，那么也就是求\(x\)到\(y'\)的距离乘上右子树大小加上\(y'\)和\(x\)内部的贡献

如果\(x\)在右子树，同理，但是注意在右子树的点跳到右子树时编号要减去左子树的大小

---

代码

#include <cstdio>
#include <cctype>
#include <map>
#define rr register
using namespace std;
typedef long long lll; const int mod=1000000007;
struct rec{int a,b; lll x,y; int w; lll siz;}tre[61];
map<pair<lll,lll>,int>uk[61]; int n,ans[61];
inline lll iut(){
	rr lll ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline void print(int ans){
	if (ans>9) print(ans/10);
	putchar(ans%10+48);
}
inline signed mo(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline signed Get(int k,lll x,lll y){
	if (x>y) x^=y,y^=x,x^=y;
	if (!k||x==y) return 0;
	rr lll A=tre[k].a,B=tre[k].b,sizA=tre[A].siz,sizB=tre[B].siz;
    if (y<sizA) return Get(A,x,y);
        else if (x>=sizA&&y>=sizA) return Get(B,x-sizA,y-sizA);
            else {
            	rr pair<lll,lll>t=make_pair(x,y);
            	if (uk[k].find(t)!=uk[k].end()) return uk[k][t];
            	return uk[k][t]=mo(mo(Get(A,tre[k].x,x),Get(B,tre[k].y,y-sizA)),tre[k].w);
	    }
}
inline signed calc(int k,lll x){
	rr pair<lll,lll>t=make_pair(x,0); if (!k) return 0;
	if (uk[k].find(t)!=uk[k].end()) return uk[k][t];
	rr int &ans=uk[k][t]; ans=0;
	rr lll A=tre[k].a,B=tre[k].b,sizA=tre[A].siz,sizB=tre[B].siz,moA=sizA%mod,moB=sizB%mod;
	if (x<sizA) ans=mo(mo(calc(tre[k].a,x),calc(tre[k].b,tre[k].y)),mo(tre[k].w,Get(tre[k].a,tre[k].x,x))*moB%mod);
	    else ans=mo(mo(calc(tre[k].a,tre[k].x),calc(tre[k].b,x-sizA)),mo(tre[k].w,Get(tre[k].b,tre[k].y,x-sizA))*moA%mod);
	return ans;
}
signed main(){
	for (rr int Test=iut();Test;--Test){
		n=iut(),tre[0].siz=1,ans[0]=0;
		for (rr int i=1;i<=n;++i)
		    tre[i]=(rec){iut(),iut(),iut(),iut(),iut(),0},
		        tre[i].siz=tre[tre[i].a].siz+tre[tre[i].b].siz;
		for (rr int i=0;i<=n;++i) uk[i].clear();
		for (rr int i=1;i<=n;++i){
			rr lll A=tre[i].a,B=tre[i].b,sizA=tre[A].siz,sizB=tre[B].siz,moA=sizA%mod,moB=sizB%mod;
			rr int t1=moA*calc(tre[i].b,tre[i].y)%mod,t2=calc(tre[i].a,tre[i].x)*moB%mod;
			ans[i]=mo(mo(mo(ans[A],ans[B]),tre[i].w*moA%mod*moB%mod),mo(t1,t2));
		}
		for (rr int i=1;i<=n;++i) print(ans[i]),putchar(10);
	}
	return 0;
}