灰色预测是对时间有关的灰色过程进行预测。通过建立相应的微分方程模型，从而预测事物未来发展趋势的状况。

由于笔者的水平不足，本章只是概括性地介绍GM（1，1）模型的理论原理，便于对初学者的初步理解

一、灰色系统

二、GM(1,1)灰色预测模型

GM(1,1)是使用原始的离散非负数据列，通过一次累加生成削弱随机性的较有规律的新的离散数据列，然后通过建立微分方程模型，得到在离散点处的解经过累减生成的原始数据的近似估计值，从而预测原始数据的后续发展。

（第一个‘1’表示微分方程是一阶的，后面的‘1’表示只有一个变量）

1.生成累加数据与紧临均值生成序列

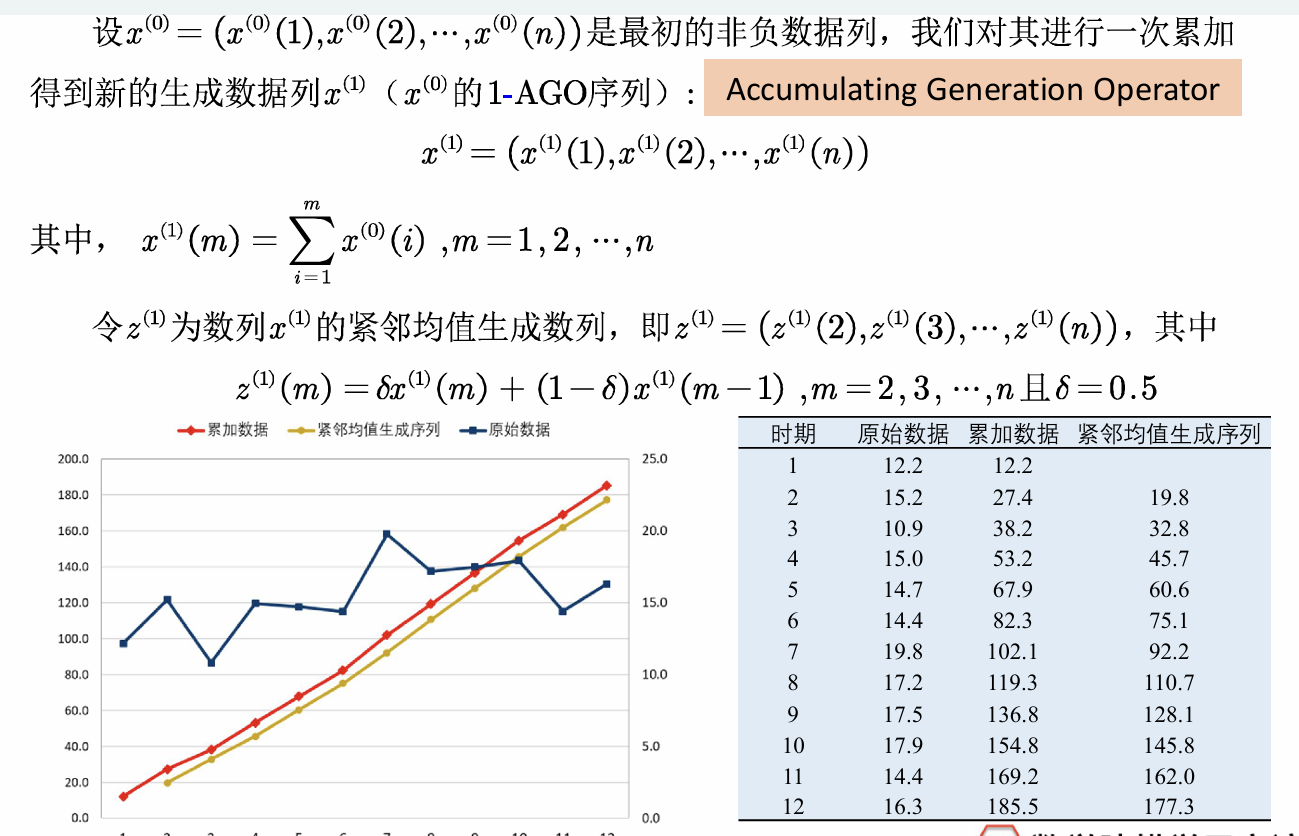
2.建立预测方程与参数估计

我们称方程x(°)(k) + az(1)(k) =b为GM(1,1)模型的基本形式(k=2,3,…,n)其中，b表示灰作用量，-a表示发展系数。

之后，建立回归方程，估计出a_hat与b_hat

3.转离散为连续，建立微分方程

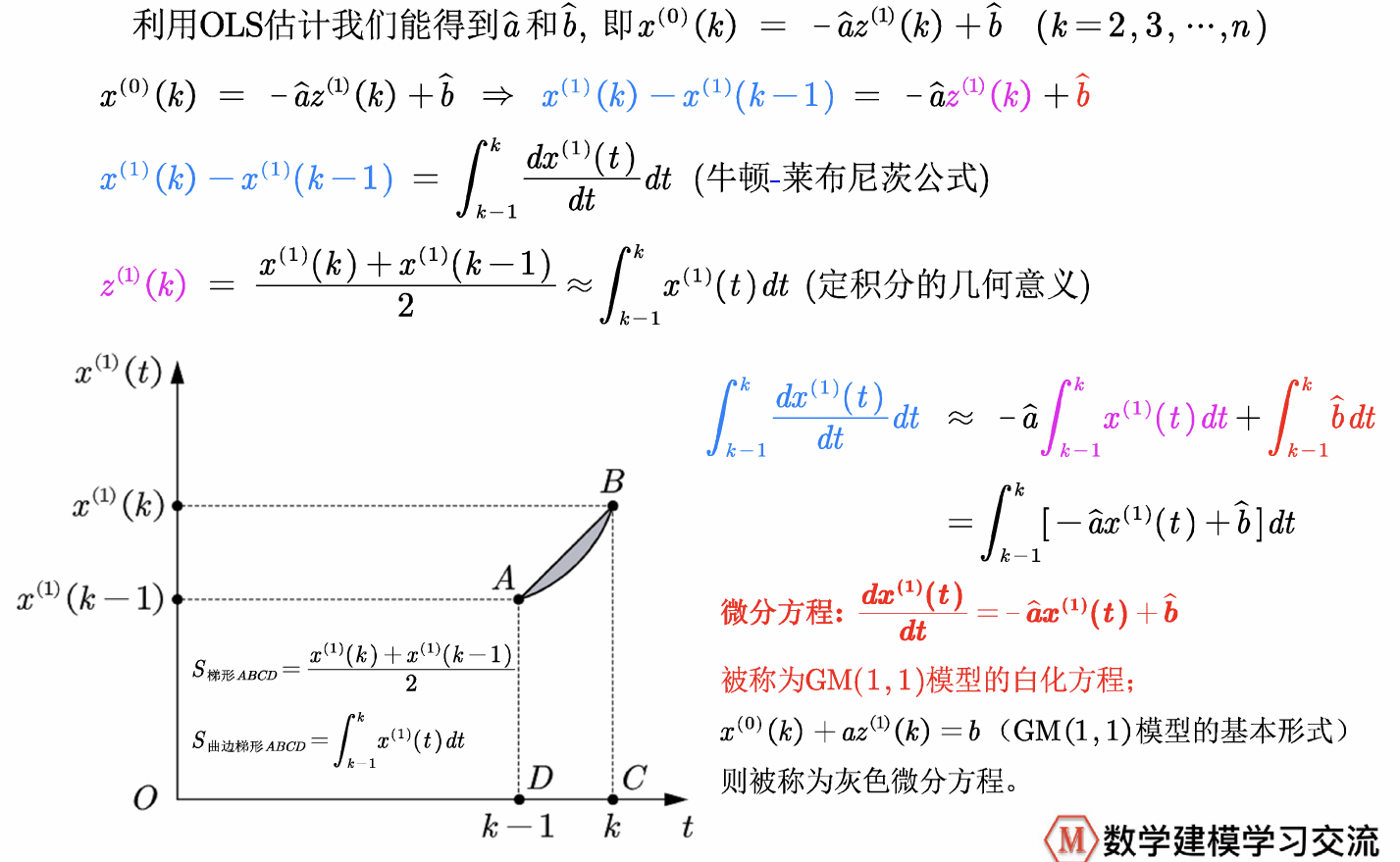
4.求解微分方程————GM(1,1)模型的本质是有条件的指数拟合

由常微分方程的求解公式，我们最后得到的结果是一个带指数项的函数，因此我们可以得出结论：GM(1,1)模型的本质是有条件的指数拟合

5.准指数规律的检验

数据具有准指数规律是使用灰色系统建模的理论基础。

(1)定义级比



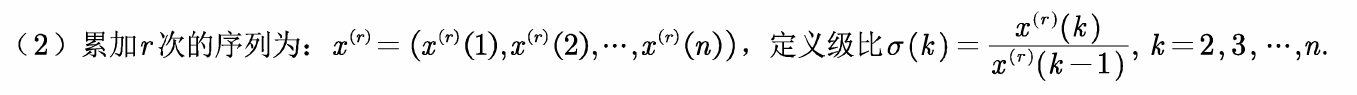
当级比所在的区间长度<0.5，则称累加r次后的序列具有准指数规律。

(3)指标转换————将级比转化为光滑比

我们通过一系列的数学转换，将级比转化为另一个指标————光滑比。当光滑比ρ<0.5时，与级比长度<0.5等价

6.发展系数与预测情形的探究

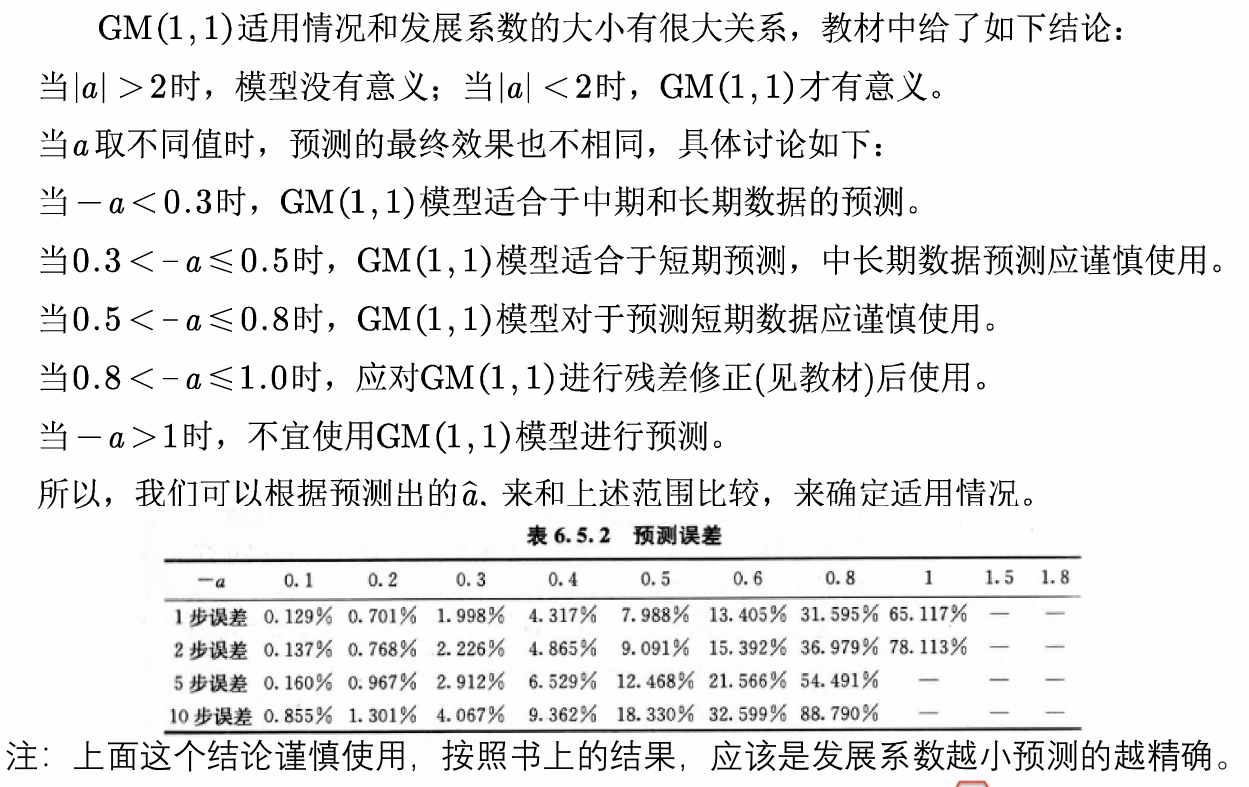
7.GM(1,1)模型的评价

使用GM(1,1)模型对未来的数据进行预测时，我们需要先检验GM(1,1)模型对原数据的拟合程度(对原始数据还原的效果)。一般有两种检验方法:

（1）残差检验

（2）级比偏差检验

7.GM(1,1)模型的拓展

简单来说，（3）与（4）就是把预测出来的值作为原始值，进行下一步的预测

8.什么时候用灰色预测？

灰色预测GM(1,1)模型的理论原理的更多相关文章

  1. python 实现 灰色预测 GM(1,1)模型 灰色系统 预测 灰色预测公式推导

    来源公式推导连接 https://blog.csdn.net/qq_36387683/article/details/88554434 关键词:灰色预测 python 实现 灰色预测 GM(1,1)模 ...

  2. 灰色预测 GM11模型

    灰色预测实现见:https://www.jianshu.com/p/a35ba96d852b from pandas import Series from pandas import DataFram ...

  3. R实现灰色预测

    1.简介 预测就是借助于对过去的探讨去推测.了解未来.灰色预测通过原始数据的处理和灰色模型的建立,发现.掌握系统发展规律,对系统的未来状态做出科学的定量预测.对于一个具体的问题,究竟选择什么样的预测模 ...

  4. 灰色预测原理及JAVA实现

    最近在做项目时,用户不想使用平均值来判断当前数据状态,想用其他的方式来分析数据的变化状态,在查找了一些资料后,想使用灰色预测来进行数据的预测.下面的内容是从网上综合下来的,java代码也做了一点改动, ...

  5. 灰色预测--matlab&python实现

    function SGrey X0 = input('请输入原始负荷数据:'); %输入原始数据 n = length(X0); %原始n年数据 %累加生成 X1 = zeros(1,n); for ...

  6. matlab批量灰色预测

    没事玩了一下matlab 发现现在网上的代码都是一组数据预测 所以我就写个批量数据的预测 顺便学习下matlab ----------------------------------我是快乐的分割线- ...

  7. [matlab] 21.灰色预测、线性回归分析模型与最小二乘回归 (转载)

    灰色预测的主要特点是只需要4个数据,就能解决历史数据少,序列的完整性以及可靠性低的问题,能将无规律的原始数据进行生成得到规律性较强的生成序列,易于检验 但缺点是只适合中短期的预测,且只适合指数级增长的 ...

  8. 用python做时间序列预测九：ARIMA模型简介

    本篇介绍时间序列预测常用的ARIMA模型,通过了解本篇内容,将可以使用ARIMA预测一个时间序列. 什么是ARIMA? ARIMA是'Auto Regressive Integrated Moving ...

  9. 数学建模-灰色预测模型GM(1,1)_MATLAB

    GM(1,1).m %建立符号变量a(发展系数)和b(灰作用量) syms a b; c = [a b]'; %原始数列 A A = [174, 179, 183, 189, 207, 234, 22 ...

  10. 【数学建模】day14-建立GM(1,1)预测评估模型应用

    学习建立GM(1,1)灰色预测评估模型,解决实际问题: SARS疫情对某些经济指标的影响问题 一.问题的提出 2003 年的 SARS 疫情对中国部分行业的经济发展产生了一定影响,特别是对部分 疫情较 ...

随机推荐

  1. mac更新nodejs

    查看本机node.js版本: node -v 清除node.js的cache:sudo npm cache clean -f 安装 n 工具:sudo npm install -g n 安装最新版本的 ...

  2. 利用pearcmd实现裸文件包含

    利用pearcmd实现裸文件包含 在 ctf 中,常常有这样一类题: 题目很简单,一般围绕一个 include 函数展开. 例: ctfshow 元旦水友赛 easy_include 这类题目没有提供 ...

  3. Java 工程文件的 .gitignore

    以下是一个排查 Java 工程文件的 .gitignore 文件示例: # Java 编译器生成的文件 *.class # Maven 生成的文件夹 target/ # Eclipse 生成的文件夹 ...

  4. docker --link容器互联

    目录 一.系统环境 二.docker容器互联概述 2.1 docker容器互联的三种方式 2.2 docker --link使用注意事项 2.3 docker --link原理 三.docker容器互 ...

  5. ENVI自动地理配准：GCP地面控制点的自动产生

      本文介绍基于ENVI软件,利用"Image Registration Workflow"工具实现栅格遥感影像自动寻找地面控制点从而实现地理配准的方法.   在ENVI手动地理配 ...

  6. Pandas学习之路【1】

    安装pandas: pip install pandas pandas读取数据: 数据类型 读取方式 csv, tsv, txt pd.read_csv Excel pd.read_excel mys ...

  7. ubuntu docker 解决sudo权限问题

    #如果还没有 docker group 就添加一个:$sudo groupadd docker#将用户加入该 group 内.然后退出并重新登录就生效啦.$sudo gpasswd -a ${USER ...

  8. ModelScope初体验

    使用环境:windows 11 前置条件:已安装 anaconda 参考文档:环境安装 step1:新建一个 conda 环境,命名为 modelscope conda create -n model ...

  9. 鸿蒙极速入门(五)-路由管理（Router）

    页面路由指在应用程序中实现不同页面之间的跳转和数据传递.HarmonyOS提供了Router模块,通过不同的url地址,可以方便地进行页面路由,轻松地访问不同的页面. 一.基础使用 Router模块提 ...

  10. java检测当前CPU负载状态的方法

    1.java检测当前CPU负载状态 在Java中,直接检测CPU负载状态并不像在操作系统命令行中那样简单,因为Java标准库并没有直接提供这样的功能.但是,我们可以通过几种方法间接地获取CPU负载信息 ...