解析Stream foreach源码

摘要：串行流比较简单，对于parallelStream，站在它背后的是ForkJoin框架。

本文分享自华为云社区《深入理解Stream之foreach源码解析》，作者：李哥技术 。

前言

Stream中的操作可以分为两大类：中间操作与结束操作。

今天要说的foreach是属于结束操作。

Stream流操作从并发上来分类，又可以分为并行流和串行流，今天就来刨根问底的看看吧。

foreach串行流

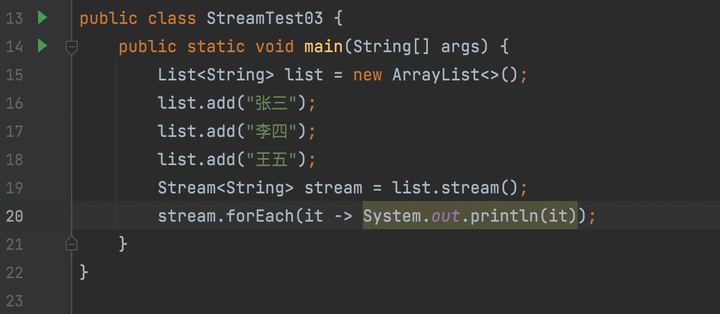
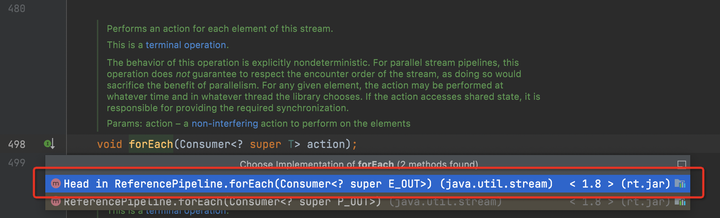
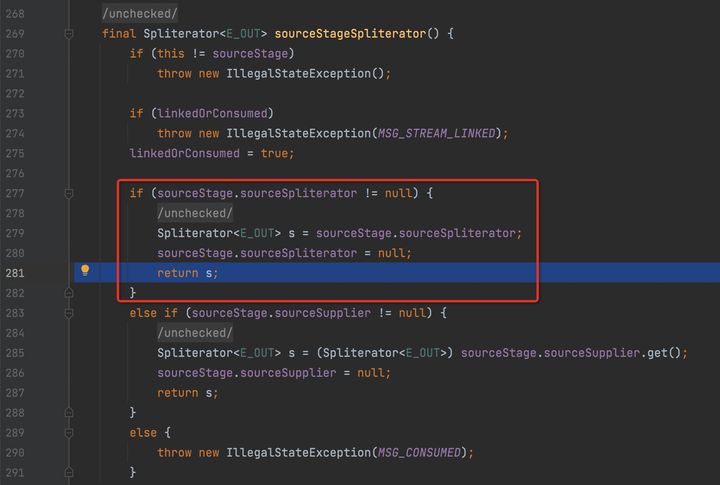
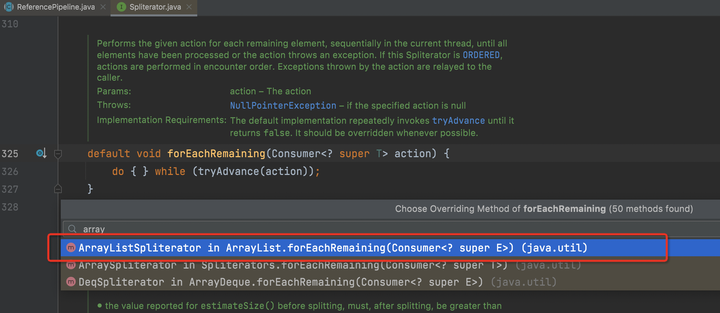
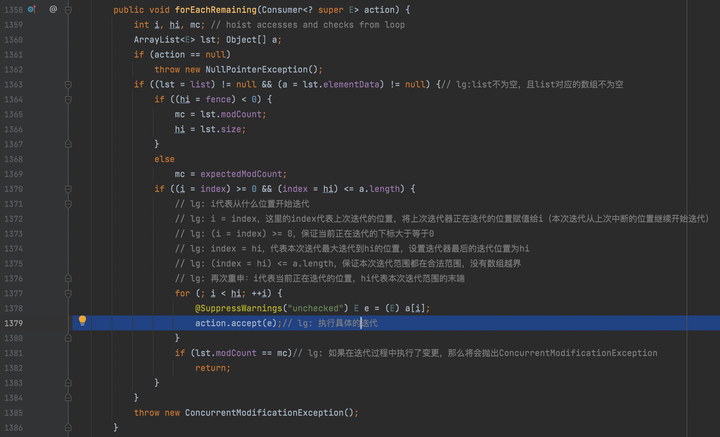
foreach并行流

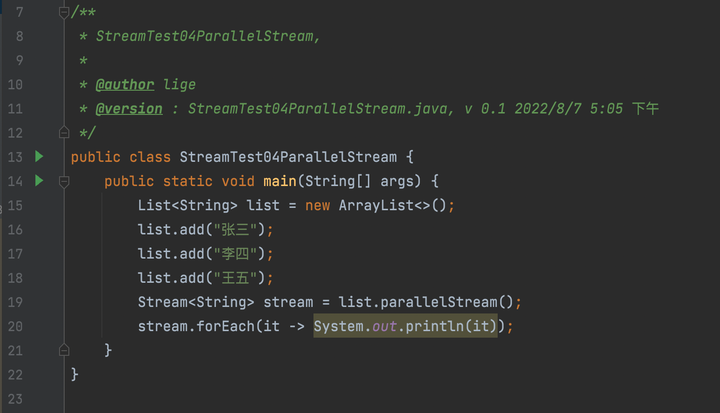
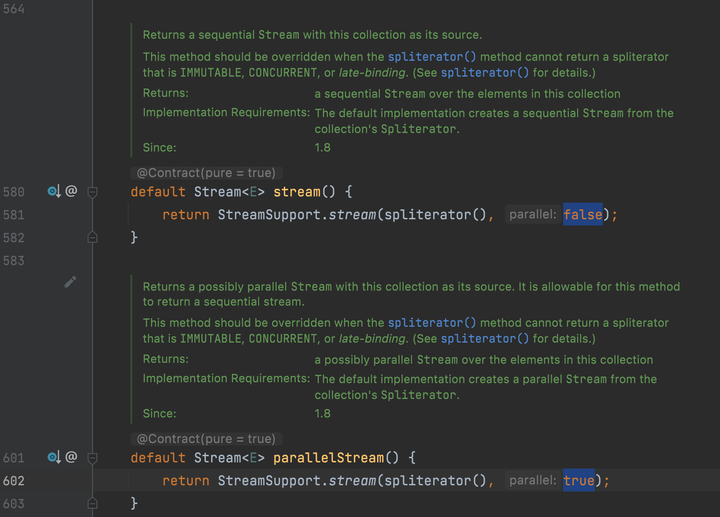
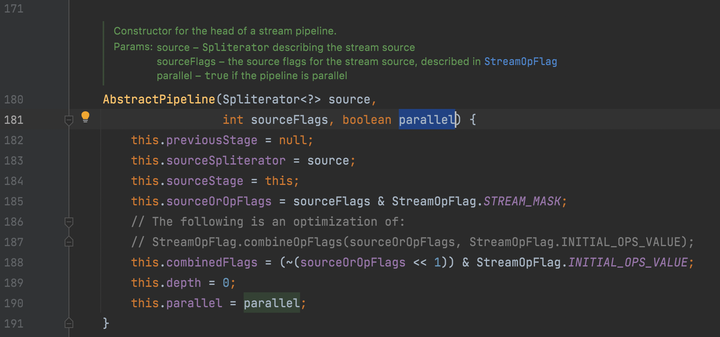
从目前来看，parallelStream(并行流)与stream(串行流)的区别仅仅是一个变量而已。别着急，让我们继续往下看。

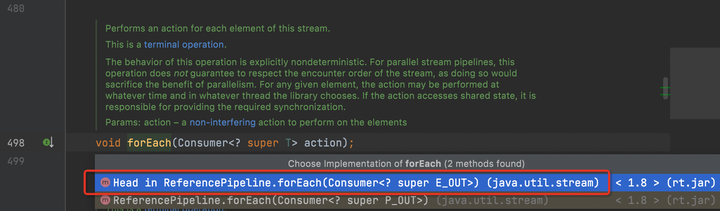
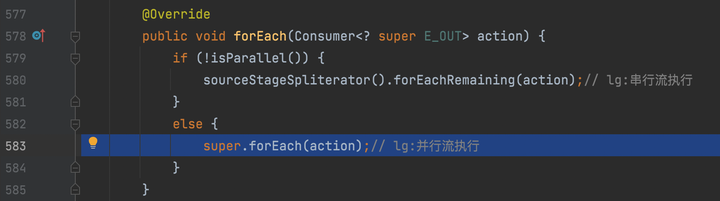
记住这里的ordered是false，因为是并行流，不可能是有序遍历。continue。

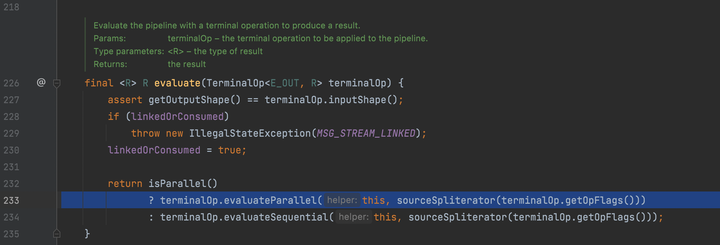
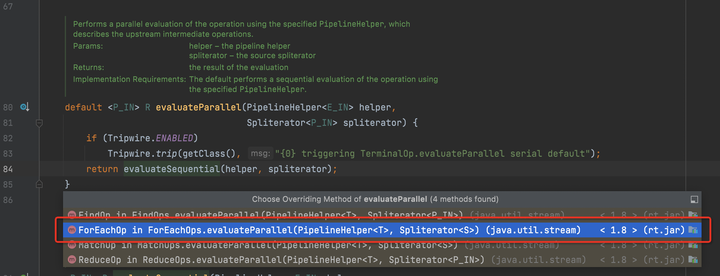
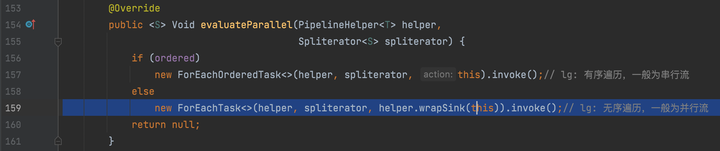
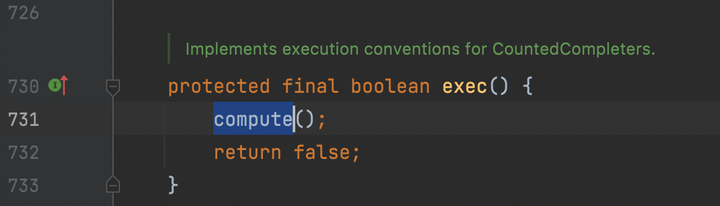
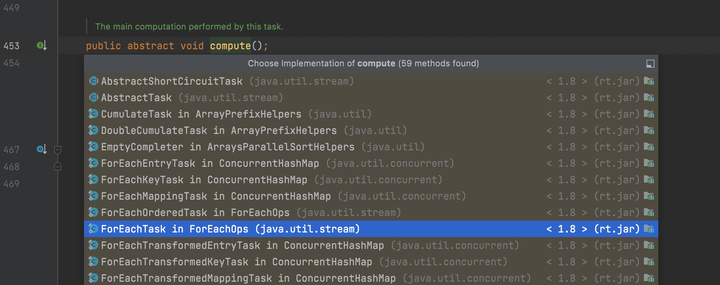
我们来简单分析一下ForEachTask类，它继承于CountedCompleter。

static final class ForEachTask<S, T> extends CountedCompleter<Void> {
}

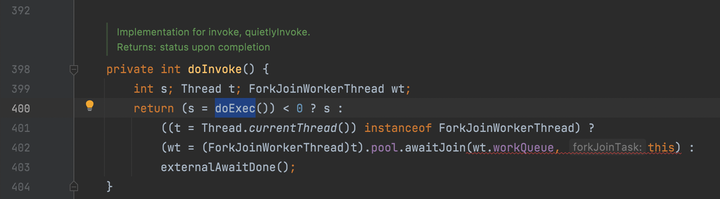
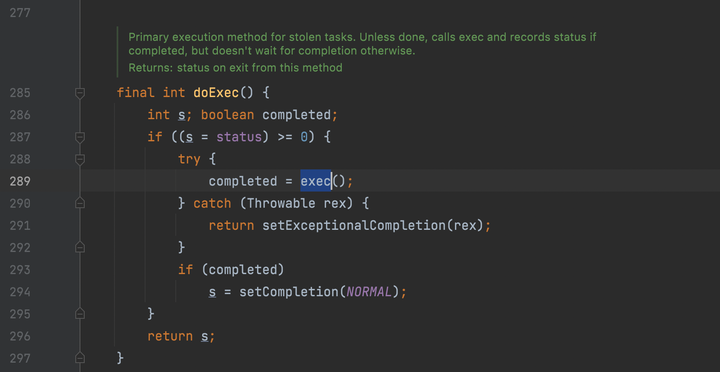
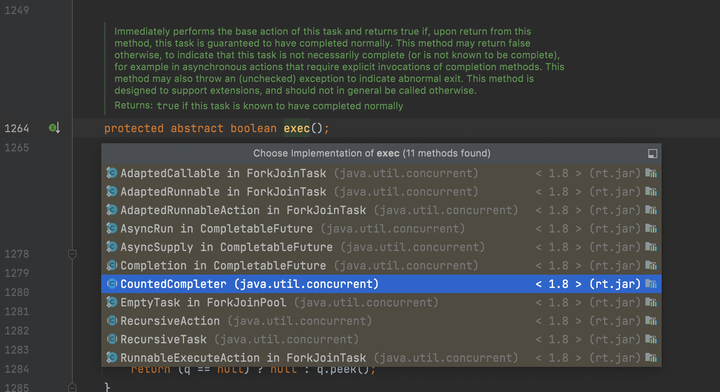
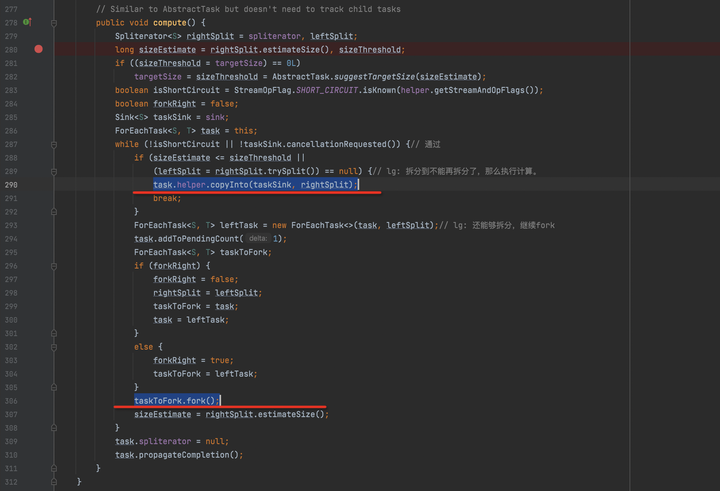
最后这里使用ForkJoin框架，利用分治法的思想，将一个大任务拆分很多个小任务去执行，最后一一汇总到大任务。

我们一路过五关斩六将，终于将它给挖穿了。不容易啊。

总结

我们简单回顾总结一下：

对于串行流：

1. 先得到ReferencePipeline.Head的Stream实现类，内部有一个拆分器，值是一个ArrayListSpliterator对象；

2. 对于并行流，当前线程直接调用ArrayListSpliterator对象的forEachRemaining方法。

对于并行流：

1. 先得到ReferencePipeline.Head的Stream实现类，内部有一个拆分器，值是一个ArrayListSpliterator对象；

2. 迭代的时候调用父类的forEach方法；

3. 构建一个ForEachTask，当前线程继续执行invoke方法；

4. 最终执行java.util.stream.ForEachOps.ForEachTask#compute方法，使用ForkJoin框架，利用commomPool、ForkJoin框架分治法的思想，使用拆分器将任务拆分成不同子任务执行；

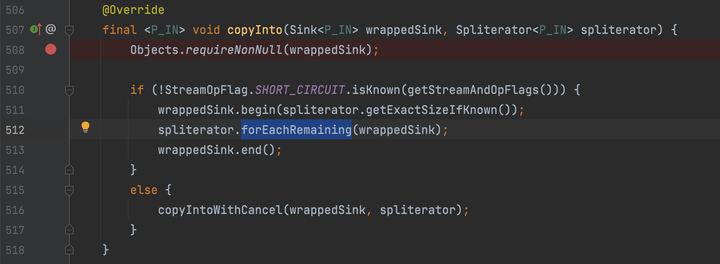
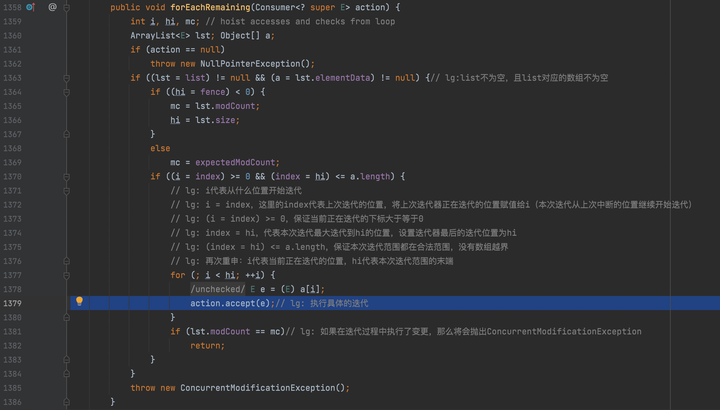
5. 对于每一个子任务都会拆分到不能再拆分为止，然后调用java.util.stream.AbstractPipeline#copyInto方法，在内部会调用不可再拆分的拆分器的forEachRemaining方法，最终调用回调用户方法action.accept(e)；

串行流比较简单，对于parallelStream，站在它背后的男人是ForkJoin框架。

ForkJoin框架是从jdk7中新特性,它同ThreadPoolExecutor一样，也实现了Executor和ExecutorService接口。ForkJoinPool主要用来使用分治法(Divide-and-Conquer Algorithm)来解决问题。Java 8为ForkJoinPool添加了一个通用线程池：commonPool，这个线程池用来处理那些没有被显式提交到任何线程池的任务。它是ForkJoinPool类型上的一个静态元素，它拥有的默认线程数量等于运行计算机上的处理器数量。所以，我们的并行流就是使用的这个公共池中的线程来执行的。

点击关注，第一时间了解华为云新鲜技术~