Trailing Zeroes (I) LightOJ - 1028（求因子个数）

题意：

给出一个N 求N有多少个别的进制的数有后导零

解析：

对于一个别的进制的数要转化为10进制 （我们暂且只分析二进制就好啦）

An * 2^(n-1) + An-1 * 2^(n-2) + ``````+ A1 * 2^1  +  A0 * 2^0  = N

因为有后导零 我们暂且只看有一个后导零的情况  即A0 = 0

那么  2 * ( An * 2^(n-2) + An01 * 2^(n-3) + `````` + A1) = N

即  An * 2^(n-2) + An-1 * 2^(n-3) + `````` + A1  =  N/2

把2替换为x进制  且 左边设为M

则 M = N / x

所以M的个数即为N的因子的个数

用算术基本定理求因子个数即可

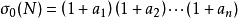
最后还要减1呀！

懒得打代码了。。。。代码原文地址：https://blog.csdn.net/zyz_3_14159/article/details/52824900

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
typedef long long ll;
bool vis[];
int prime[],cnt;
void getprime()
{
    cnt=;
    int i,j;
    for(i=;i<=;i++)
    {
        if(!vis[i])
            prime[cnt++]=i;
        for(j=*i;j<=;j+=i)
            vis[j]=;
    }
}
ll fun(ll n)
{
    ll ans=;
    int num,i;
    for(i=;i<cnt&&prime[i]*prime[i]<=n;i++)
    {
        if(n%prime[i]==)
        {
            num=;
            while(n%prime[i]==)
            {
                num++;
                n/=prime[i];
            }
            ans*=(num+);
        }
    }
    if(n>)
        ans*=;
    return ans-;
}
int main()
{
    int cas,c;
    ll n;
    getprime();
    scanf("%d",&cas);
    for(c=;c<=cas;c++)
    {
        scanf("%lld",&n);
        if(n!=)
        printf("Case %d: %lld\n",c,fun(n));
        else
        printf("Case %d: 0\n",c);
    }
    return ;
}