DSU模板(树的启发式合并)

With dsu on tree we can answer queries of this type:

How many vertices in subtree of vertex v has some property in O(n lg n) time (for all of the queries).

For example:

Given a tree, every vertex has color. Query is how many vertices in subtree of vertex v are colored with color c?

要点：记录每棵子树的大小，启发式合并。

模板整理如下：

1. easy to code but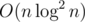

 //O(nlognlogn)

 map<int, int> *cnt[maxn];

 void dfs(int v, int p){

     int mx = -, bigChild = -;

     for(auto u : g[v])

        if(u != p){

            dfs(u, v);

            if(sz[u] > mx)

                mx = sz[u], bigChild = u;

        }

     if(bigChild != -)

         cnt[v] = cnt[bigChild];

     else

         cnt[v] = new map<int, int> ();

     (*cnt[v])[ col[v] ] ++;

     for(auto u : g[v])

        if(u != p && u != bigChild){

            for(auto x : *cnt[u])

                (*cnt[v])[x.first] += x.second;

        }

     //now (*cnt)[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.

 }

2. easy to code and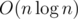

 vector<int> *vec[maxn];

 int cnt[maxn];

 void dfs(int v, int p, bool keep){

     int mx = -, bigChild = -;

     for(auto u : g[v])

        if(u != p && sz[u] > mx)

            mx = sz[u], bigChild = u;

     for(auto u : g[v])

        if(u != p && u != bigChild)

            dfs(u, v, );

     if(bigChild != -)

         dfs(bigChild, v, ), vec[v] = vec[bigChild];

     else

         vec[v] = new vector<int> ();

     vec[v]->push_back(v);

     cnt[ col[v] ]++;

     for(auto u : g[v])

        if(u != p && u != bigChild)

            for(auto x : *vec[u]){

                cnt[ col[x] ]++;

                vec[v] -> push_back(x);

            }

     //now (*cnt)[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.

     // note that in this step *vec[v] contains all of the subtree of vertex v.

     if(keep == )

         for(auto u : *vec[v])

             cnt[ col[u] ]--;

 }

3. heavy-light decomposition style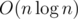

 int cnt[maxn];

 bool big[maxn];

 void add(int v, int p, int x){

     cnt[ col[v] ] += x;

     for(auto u: g[v])

         if(u != p && !big[u])

             add(u, v, x)

 }

 void dfs(int v, int p, bool keep){

     int mx = -, bigChild = -;

     for(auto u : g[v])

        if(u != p && sz[u] > mx)

           mx = sz[u], bigChild = u;

     for(auto u : g[v])

         if(u != p && u != bigChild)

             dfs(u, v, );  // run a dfs on small childs and clear them from cnt

     if(bigChild != -)

         dfs(bigChild, v, ), big[bigChild] = ;  // bigChild marked as big and not cleared from cnt

     add(v, p, );

     //now cnt[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.

     if(bigChild != -)

         big[bigChild] = ;

     if(keep == )

         add(v, p, -);

 }

4. My invented style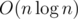

 This implementation for "Dsu on tree" technique is new and invented by me. This implementation is easier to code than others. Let st[v] dfs starting time of vertex v, ft[v] be it's finishing time and ver[time] is the vertex which it's starting time is equal to time.

 int cnt[maxn];

 void dfs(int v, int p, bool keep){

     int mx = -, bigChild = -;

     for(auto u : g[v])

        if(u != p && sz[u] > mx)

           mx = sz[u], bigChild = u;

     for(auto u : g[v])

         if(u != p && u != bigChild)

             dfs(u, v, );  // run a dfs on small childs and clear them from cnt

     if(bigChild != -)

         dfs(bigChild, v, );  // bigChild marked as big and not cleared from cnt

     for(auto u : g[v])

     if(u != p && u != bigChild)

         for(int p = st[u]; p < ft[u]; p++)

         cnt[ col[ ver[p] ] ]++;

     cnt[ col[v] ]++;

     //now cnt[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.

     if(keep == )

         for(int p = st[v]; p < ft[v]; p++)

         cnt[ col[ ver[p] ] ]--;

 }

时间复杂度分析

4. My invented style

考虑每个节点最多会被清零几次？

显然被清零的次数即为该节点到根节点的链上轻儿子的个数

联系树链剖分，任意一个节点到根节点的链最多被划分为O(logn)段重链，最多被清零O(logn)次.

故时间复杂度为O(nlogn).

2, 3, 4时间复杂度分析类似.

启发式合并算法复杂度总结

线段树合并 => O(nlogU), U为线段树权值域，从势能分析，合并的复杂度为O(总节点数减小的个数)

平衡树合并+树链剖分+单次插入删除O(logn) => O(nlognlogn)

平衡树合并+树链剖分+单次插入删除O(1) => O(nlogn)

set合并 => O(nlognlogn), 显然set合并复杂度不会高于multiset(平衡树)合并复杂度