[论文阅读笔记] Are Meta-Paths Necessary, Revisiting Heterogeneous Graph Embeddings

[论文阅读笔记] Are Meta-Paths Necessary? Revisiting Heterogeneous Graph Embeddings

本文结构

解决问题
主要贡献
算法原理
参考文献

(1) 解决问题

传统的异构网络中的随机游走常常偏向于采样节点数比较多的节点类型。为了克服该问题，metapath2vec提出了基于元路径的随机游走，然而使用元路径策略要么要求先验知识，要么需要通过额外的操作来结合所有短的元路径到一个预定义的序列长度（如多元路径的情况，如何取舍，哪个更重要？）。本文基于该以上传统随机游走存在的偏向性问题出发，提出了不使用元路径策略的另外一种解决方法。

(2) 主要贡献

Contribution： 本篇论文提出了一种基于随机游走的异构网络嵌入算法JUST（不使用元路径），设计了JUmp和STay两个策略来以一种更有效的方式克服上述提出的传统异构网络随机游走偏差的问题。

(3) 算法原理

JUST算法框架主要包含两个部分：首先在图上做基于JUMP和STAY策略的随机游走，其次将得到的节点序列输入Skip-Gram模型学习节点表示向量嵌入(不再赘述)。

基于JUMP和STAY策略的随机游走

相比于同构网络，异构网络中的存在多种节点类型，该论文在传统异构图网络随机游走的基础之上，设计了两种策略来选择随机游走中下一跳节点的类型，即Jump和Stay策略。

1. Jump（跳转策略）： 即随机游走下一跳跳转到其他节点类型上去，假设下一跳节点类型为q，则所有与当前节点有边的且属于节点类型q的邻居节点都是下一跳节点的候选集。

2. Stay（停留策略）： 即随机游走下一跳停留在当前节点的节点类型上，则所有与当前节点有连边且与当前节点同类型的邻居节点为下一跳节点的候选集。

基于以上两种策略，我们需要确定以下细节来控制随机游走：何时jump何时stay？jump的时候，要jump到哪个节点类型合适？

1. 何时jump何时stay？： stay和jump的概率设计如下，

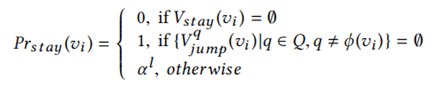
一共包括三种情况：

（1）如果没有与当前节点同类型的邻居节点，那stay不了，就jump。

（2）如果没有与当前节点不同类型的邻居节点，那jump不了，就stay。

（3）如果既有与当前节点同类型的邻居又有不同类型的邻居，那以α的L次方确定stay和Junp的概率。α为初始的stay概率（超参数），L为到目前为止连续访问同一类型节点的次数（为了防止随机游走连续使用停留策略采样同一类型的节点，因此设计以指数概率衰减）。

2. jump的时候，要jump到哪个节点类型合适？： 以如下方式构造待选节点类型集合：

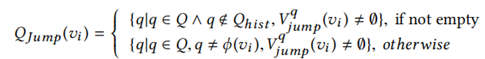
一共包含两种情况：

（1）节点类型q在最近没被选择过（构造一个m大小的队列来存储最近被选择跳转过的节点类型）并且当前节点的q类型节点邻居非空，满足该要求节点类型的为待选节点类型。以下为一个m=2的例子 (Q_hist存储最近被选择跳转的m=2个节点类型，下一跳节点类型跳转就选不到P和A两个类型了)：

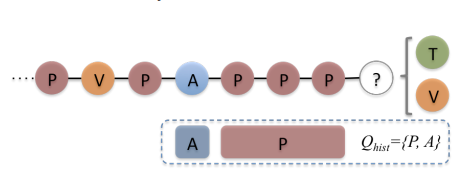
（2）如果由上述要求构造出来的待选节点类型集合是空的（即没有满足上述条件的节点类型），那就放松条件重新构造该集合。即不和当前节点的节点类型相同的其他节点类型都作为待选节点类型。

构造完待选节点类型之后，下一跳待转移的节点类型从该集合中随机采样即可，选完节点类型之后选择具体节点也是随机的。

通过以上方式生成异构网络上的随机游走序列之后，采用Skip-Gram模型训练节点向量即可。

(4) 参考文献

Hussein R, Yang D, Cudré-Mauroux P. Are Meta-Paths Necessary? Revisiting Heterogeneous Graph Embeddings[A]. Proceedings of the 27th ACM International Conference on Information and Knowledge Management[C]. 2018: 437–446.