Taylor公式原来可以这么简单

1、Taylor公式

解决：含有高阶导数的中值定理或定积分、极限运算等题目

条件：f(x)在x=x₀领域内(n+1)阶可导

结论：f(x)=P_n(x)+R_n(x)

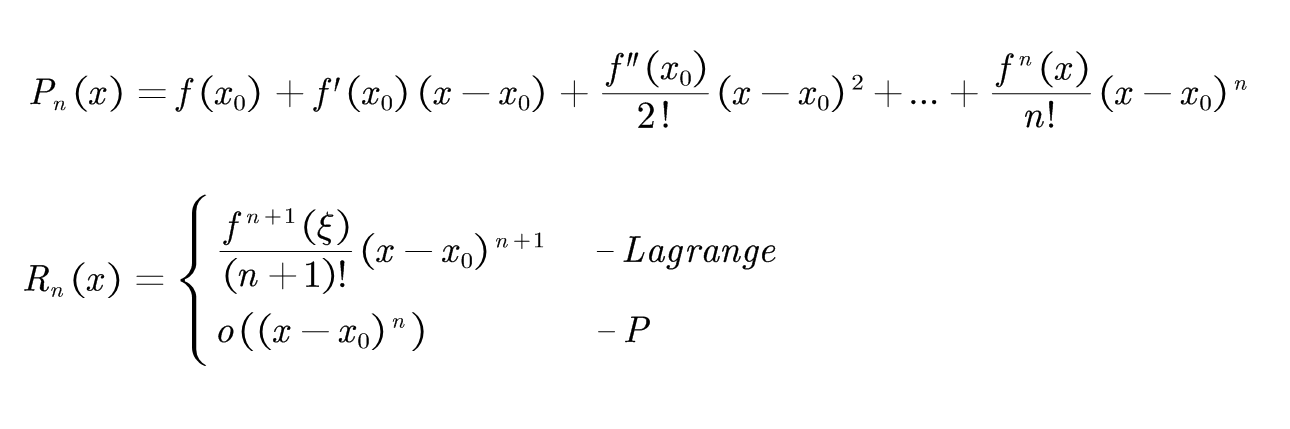
2、x和x₀的取值

3、Taylor在中值定理中的运用

如下情况我们可以尝试使用（或Lagrange完全用不了）：

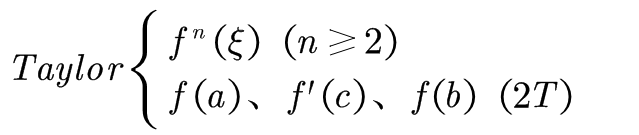
或给定f(x)及区间[a,b],将f(a)、f(b)分别在(a+b)/2处展开或将f((a+b)/2)分别在a、b两处展开，要根据证明结果来判断怎样展开。

可见完成步骤如下：

• 分析要使用Taylor
• 写出泰勒公式（一般都是Lagrange形式）
• 根据情况，使用加减、绝对值、介值定理等条件归纳
• 整合得出证明成立

4、Taylor在定积分中的运用

如下情况我们可以尝试使用：

可见完成步骤如下：

• 分析要使用Taylor，用f还是F
• 写出泰勒公式（一般都是Lagrange形式）
• 根据情况，使用积分、加减、绝对值、介值定理等条件归纳
• 整合得出证明成立

5、Taylor在极限中的运用

就是我们俗称的泰勒公式（皮亚诺形式），记住如下自推即可：

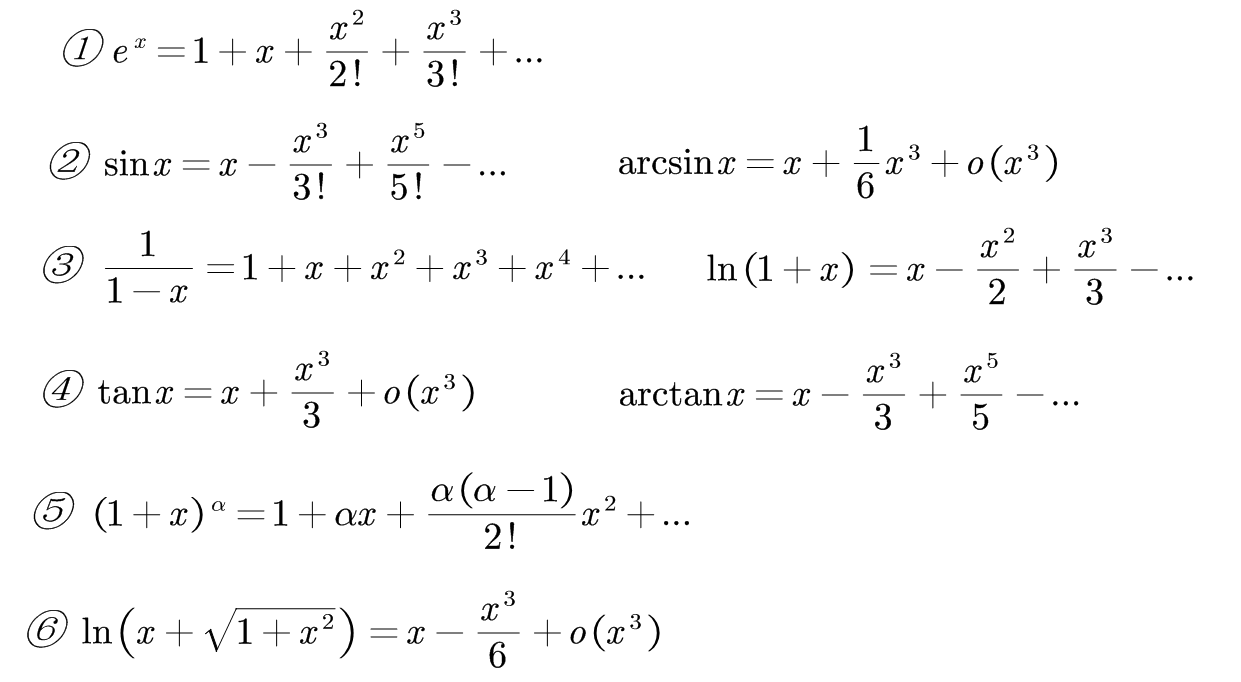
极大程度简化了极限的运算，展示一道题有兴趣可以算一下（答案可以百度哈）

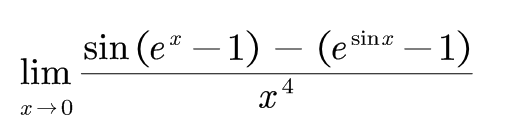
先写到这，还会有补充。