Interesting Fibonacci(hdu 2814)

Interesting Fibonacci

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1071    Accepted Submission(s): 229

Problem Description

In
mathematics, the Fibonacci numbers are a sequence of numbers named
after Leonardo of Pisa, known as Fibonacci (a contraction of filius
Bonaccio, "son of Bonaccio"). Fibonacci's 1202 book Liber Abaci
introduced the sequence to Western European mathematics, although the
sequence had been previously described in Indian mathematics.
  The
first number of the sequence is 0, the second number is 1, and each
subsequent number is equal to the sum of the previous two numbers of the
sequence itself, yielding the sequence 0, 1, 1, 2, 3, 5, 8, etc. In
mathematical terms, it is defined by the following recurrence relation:

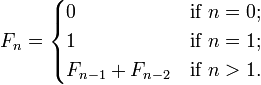
That
is, after two starting values, each number is the sum of the two
preceding numbers. The first Fibonacci numbers (sequence A000045 in
OEIS), also denoted as F[n];
F[n] can be calculate exactly by the following two expressions:


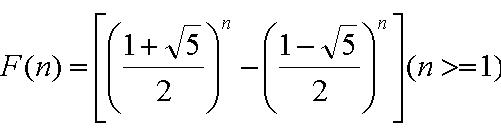
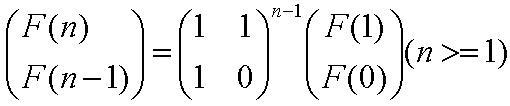
A
Fibonacci spiral created by drawing arcs connecting the opposite
corners of squares in the Fibonacci tiling; this one uses squares of
sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34;

So you can see how interesting the Fibonacci number is.
Now AekdyCoin denote a function G(n)

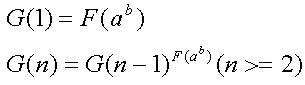
Now your task is quite easy, just help AekdyCoin to calculate the value of G (n) mod C

 

Input

The
input consists of T test cases. The number of test cases (T is given in
the first line of the input. Each test case begins with a line
containing A, B, N, C (10<=A, B<2^64, 2<=N<2^64,
1<=C<=300)

 

Output

For
each test case, print a line containing the test case number( beginning
with 1) followed by a integer which is the value of G(N) mod C

 

Sample Input

1
17 18446744073709551615 1998 139

 

Sample Output

Case 1: 120

 

Author

AekdyCoin

 思路:欧拉函数；

G（n）= F（a^b）^((F(a^b))^(N-1));然后，找一下数列的循环节，然后应为a^b>300,所以直接用欧拉降幂，(（F（a^b）^(N-1)）%oula[C] + oula[C]);因为F（a^b）^(N-1) > oula[C];

这样幂数就就降下来了。

  1 #include<stdio.h>
  2 #include<algorithm>
  3 #include<stdlib.h>
  4 #include<queue>
  5 #include<iostream>
  6 #include<string.h>
  7 #include<math.h>
  8 using namespace std;
  9 typedef unsigned long long LL;
 10 bool prime[400];
 11 int ans[400];
 12 int oula[400];
 13 int ff[30];
 14 typedef struct node
 15 {
 16         LL m[2][2];
 17         node()
 18         {
 19                 memset(m,0,sizeof(m));
 20         }
 21 } maxtr;
 22 int f[10000];
 23 int fin(LL n);
 24 LL quick(LL n,LL m,LL mod);
 25 int main(void)
 26 {
 27         memset(prime,0,sizeof(prime));
 28         int i,j;
 29         for(i = 0; i <= 300; i++)
 30         {
 31                 oula[i] = i;
 32         }
 33         int cn = 0;
 34         for(i = 2; i <= 300; i++)
 35         {
 36                 if(!prime[i])
 37                 {
 38                         ans[cn++] = i;
 39                         for(j = i; (i*j) <= 300; j++)
 40                         {
 41                                 prime[i*j] = true;
 42                         }
 43                 }
 44         }//printf("%d\n",cn);
 45         for(i = 0; i < cn; i++)
 46         {
 47                 for(j = 1; ans[i]*j <= 300; j++)
 48                 {
 49                         oula[ans[i]*j]/=ans[i];
 50                         oula[ans[i]*j]*=(ans[i] - 1);
 51                 }
 52         }
 53         ff[0] = 0;
 54         ff[1] = 1;
 55         for(i = 2; i <= 20; i++)
 56         {
 57                 ff[i] = ff[i-1]+ff[i-2];
 58         }
 59         //printf("%d\n",ff[20]);
 60         LL A,B,N,C;
 61         int T;
 62         scanf("%d",&T);
 63         int __ca = 0;
 64         while(T--)
 65         {
 66                 scanf("%llu %llu %llu %llu",&A,&B,&N,&C);
 67                 {
 68                         printf("Case %d: ",++__ca);
 69                         if(C == 1)
 70                                 printf("0\n");
 71                         else
 72                         {
 73                                 int k = fin(C);
 74                                 LL ask = quick(A,B,(LL)k);
 75                                 LL c = (LL)f[ask];
 76                                 if(c == 0)
 77                                         printf("0\n");
 78                                 else
 79                                 {
 80                                         LL v = A;
 81                                         LL x = B;
 82                                         int flag = 0;
 83                                         {
 84                                                 int u = fin((LL)oula[C]);
 85                                                 LL avk = quick(A,B,(LL)u);
 86                                                 LL app = (LL)f[avk];
 87                                                 LL ni = quick(app,N-1,(LL)oula[C]);
 88                                                 ni = ni + (LL)oula[C];
 89                                                 printf("%llu\n",quick(c,ni,C));
 90                                         }
 91                                 }
 92                         }
 93                 }
 94         }
 95         return 0;
 96 }
 97 int fin(LL n)
 98 {
 99         f[0] = 0;
100         f[1] = 1;
101         int id;
102         int i;
103         for(i = 2; i < 5000; i++)
104         {
105                 f[i] = f[i-1]+f[i-2];
106                 f[i]%=n;
107                 if(f[i] == f[1]&&f[0] == f[i-1])
108                 {
109                         id = i-2;
110                         break;
111                 }
112         }//printf("%d\n",id);
113         return id+1;
114 }
115 LL quick(LL n,LL m,LL mod)
116 {
117         LL ak = 1;
118         n%=mod;
119         while(m)
120         {
121                 if(m&1)
122                 {
123                         ak = ak*n%mod;
124                 }
125                 n = n*n%mod;
126                 m/=2;
127         }
128         return ak;
129 }