35、搜索插入位置 | 算法（leetode，附思维导图 + 全部解法）300题

零 标题：算法（leetode，附思维导图 + 全部解法）300题之（35）搜索插入位置

一 题目描述

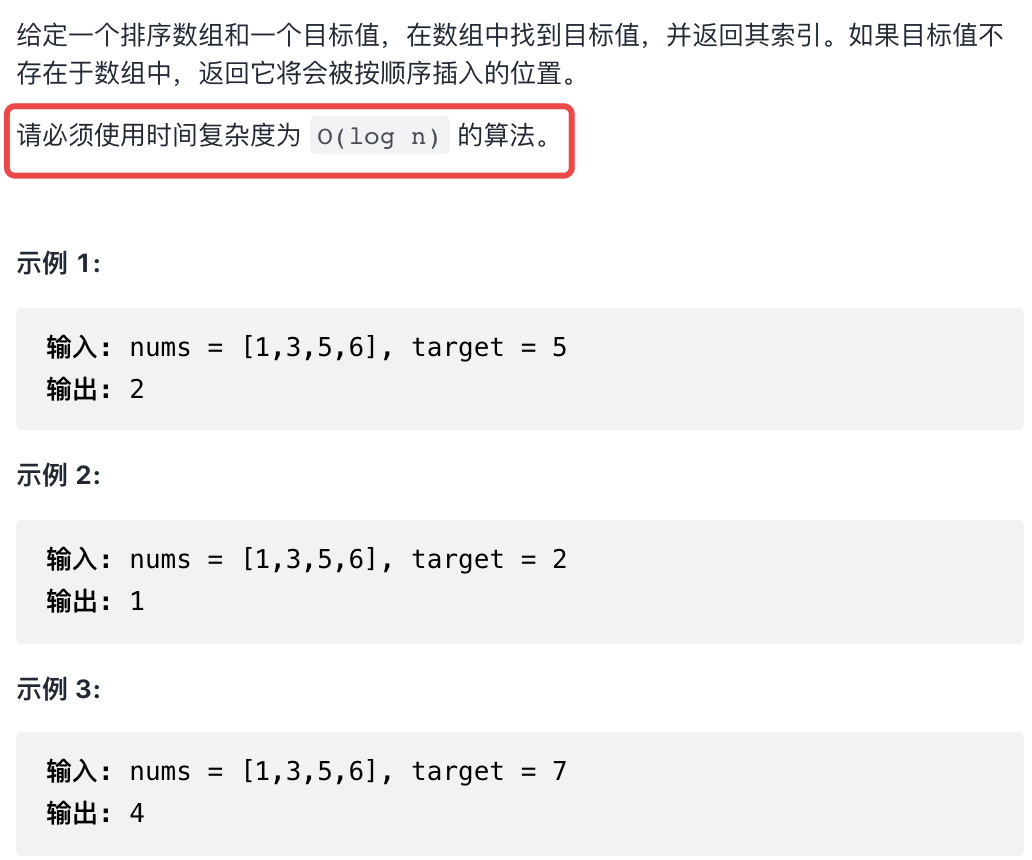
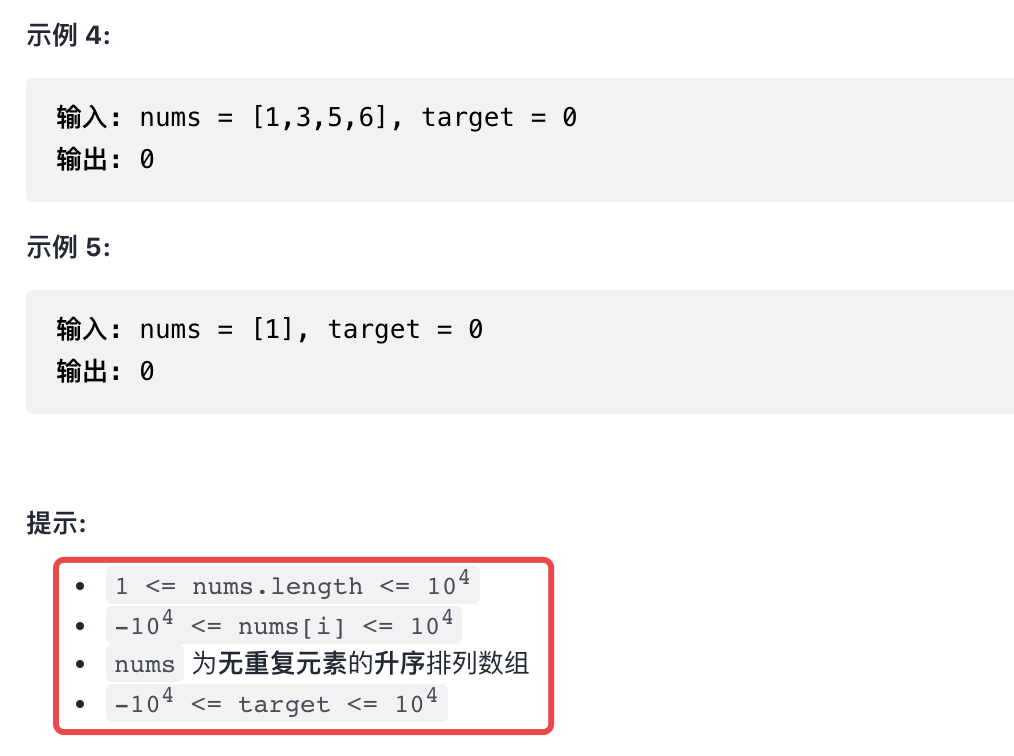
二 解法总览（思维导图）

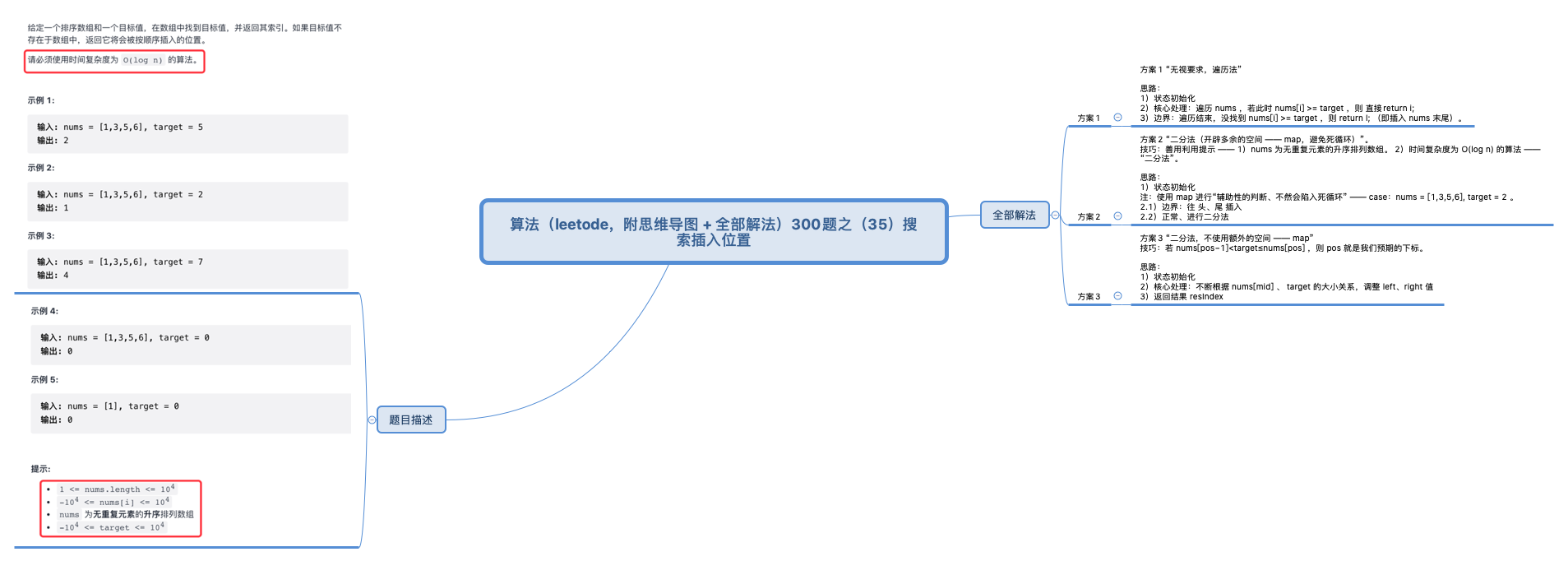
三 全部解法

1 方案1

1)代码：

// 方案1 “无视要求，遍历法”

// 思路：
// 1）状态初始化
// 2）核心处理：遍历 nums ，若此时 nums[i] >= target ，则 直接return i;
// 3）边界：遍历结束，没找到 nums[i] >= target ，则 return l; （即插入 nums 末尾）。
var searchInsert = function(nums, target) {
    // 1）状态初始化
    const l = nums.length;

    // 2）核心处理：遍历 nums ，若此时 nums[i] >= target ，则 直接return i;
    for (let i = 0; i < l; i++) {
        if (nums[i] >= target) {
            return i;
        }
    }

    // 3）边界：遍历结束，没找到 nums[i] >= target ，则 return l; （即插入 nums 末尾）。
    return l;
};

2 方案2

1)代码：

// 方案2 “二分法（开辟多余的空间 —— map，避免死循环）”。
// 技巧：善用利用提示 —— 1）nums 为无重复元素的升序排列数组。 2）时间复杂度为 O(log n) 的算法 —— “二分法”。

// 思路：
// 1）状态初始化
// 注：使用 map 进行“辅助性的判断、不然会陷入死循环” —— case：nums = [1,3,5,6], target = 2 。
// 2.1）边界：往 头、尾 插入
// 2.2）正常、进行二分法
var searchInsert = function(nums, target) {
    // 1）状态初始化
    // 注：使用 map 进行“辅助性的判断、不然会陷入死循环” —— case：nums = [1,3,5,6], target = 2 。
    const l = nums.length;
    let left = 0,
        right = l - 1,
        map = new Map();

    // 2.1）边界：往 头、尾 插入
    if (target <= nums[left]) {
        return 0;
    }
    else if (target === nums[right]){
        return l - 1;
    }
    else if (target > nums[right]){
        return l;
    }
    // 2.2）正常、进行二分法
    else {
        while (left <= right) {
            const tempStr = `${left}#${right}`;
            if (map.has(tempStr)) {
                return left + 1;
            }
            else {
                map.set(tempStr, 1)
            }

            let mid = parseInt((left + right) / 2);
            if (nums[mid] === target) {
                return mid;
            }
            else if (nums[mid] > target) {
                right = mid;
            }
            else {
                left = mid;
            }
        }
    }
}

3 方案3

1)代码：

// 方案3 “二分法，不使用额外的空间 —— map”
// 技巧：若 nums[pos−1]<target≤nums[pos] ，则 pos 就是我们预期的下标。

// 思路：
// 1）状态初始化
// 2）核心处理：不断根据 nums[mid] 、 target 的大小关系，调整 left、right 值
// 3）返回结果 resIndex
var searchInsert = function(nums, target) {
    // 1）状态初始化
    const l = nums.length;
    let left = 0,
        right = l - 1,
        resIndex = l;

    // 2）核心处理：不断根据 nums[mid] 、 target 的大小关系，调整 left、right 值
    while (left <= right) {
        // 注：等同于 const mid = ((right - left) >> 1) + left;
        const mid = parseInt((left + right) / 2);
        if (nums[mid] >= target) {
            resIndex = mid;
            right = mid - 1;
        }
        else {
            left = mid + 1;
        }
    }

    // 3）返回结果 resIndex
    return resIndex;
}

四 更多

1 刷题进度

1）LeetCode：307 / 2390 。

2）《剑指offer》：66 / 66 。

3）相关学习资料与笔记汇总：
https://github.com/CYBYOB/algorithm-leetcode/tree/master/资料%26笔记 。

4）注：所有题目均有 2-5种 左右的解法，后续还将不断更新题目 & 题解。
敬请期待~
也欢迎大家进群一起 学习、交流、刷题&拿高薪~

2 GitHub - LeetCode项目仓库

0）本项目地址：
https://github.com/CYBYOB/algorithm-leetcode 。
目标、愿景：
让每个人都能拥有一定的算法能力、以应对面试中（会举一反三的同学还可以将其融入自己的肌肉和血液，甚至能够赋能于公司的业务和技术）的算法。

本人每周仍在不断的更新 —— 保证每周都有新的题目、题解方案刺激着您的神经 和 刷题欲望。
欢迎对算法感兴趣的同学加入我们的社群。
QQ群： 933919972 ；
作者QQ： 1520112971 ；
作者VX： c13227839870（可拉您进群、一起学习与交流~） 。

3 作者标签

1）“BAT里1名小小的伪全栈工程师，主攻前端，偶尔写点后端”。

2）2019年的微信小程序应用开发赛 - 全国三等奖；
2019CODA比赛 - 前 17/211 强 且 荣获“优秀团队”称号 等。

3）“半自媒体人”，
在校期间、个人公众号（IT三少。新自媒体（公众号）号： 码农三少 ）
在半年内实现了0到5.8K+的粉丝增长等。