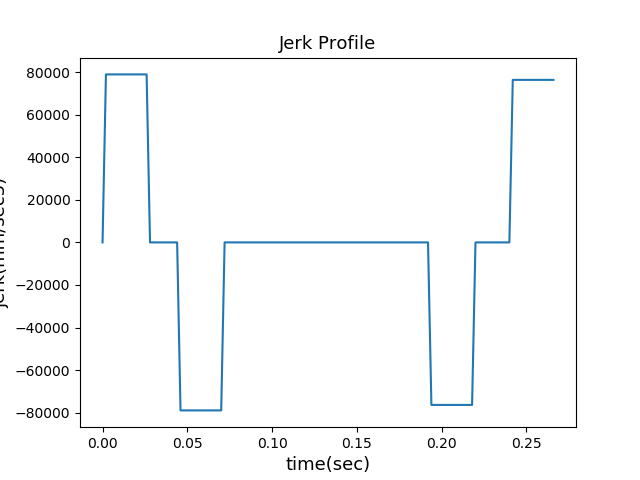
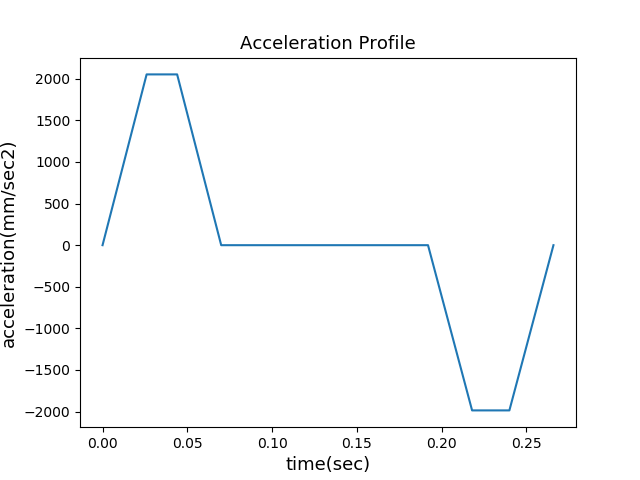
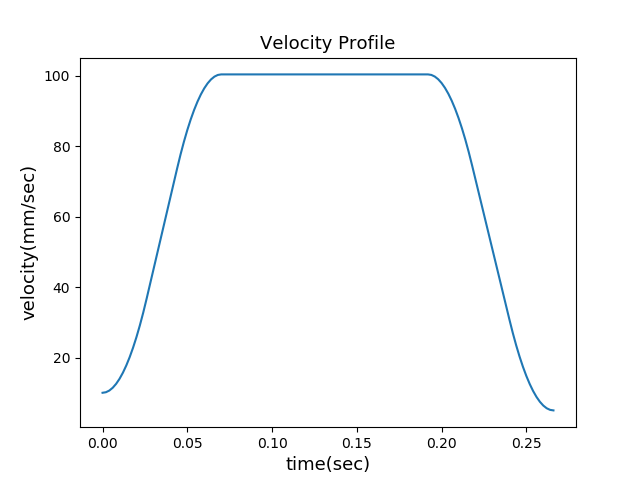
3rd S-curve velocity profile
3rd S-curve
 (1)
(1)
 (2)
(2)
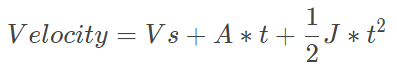 (3)
(3)

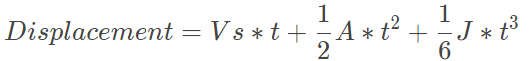 (4)
(4)
完整的三次S曲线包括上面的七个阶段。前面三个阶段为加速阶段,从初始速度Vs加速到Vmax:
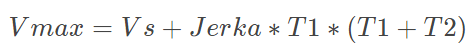 (5)
(5)
整个加速阶段的位移为:
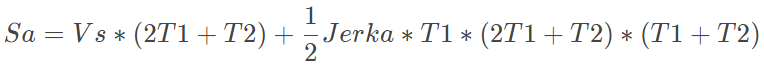 (6)
(6)
后面三个阶段为减速阶段:
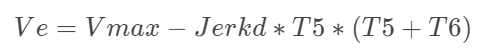 (7)
(7)
 (8)
(8)
也可以看作为反向加速阶段,即速度从最终速度Ve加速到Vmax:
 (9)
(9)
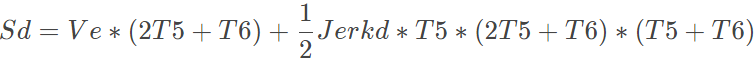 (10)
(10)
中间的阶段为匀速阶段:
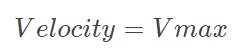
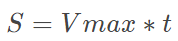 (11)
(11)
但是在实际中,受限于Vs,Ve,以及位移L,整条速度曲线并不包含完整的七个阶段,通常Jerka = Jerkd = Jerk。那么求速度曲线可以转换为以下数学问题:已知Vs,Ve,L,Amax,Jerk,Fmax,求解下面的四元三次方程组:
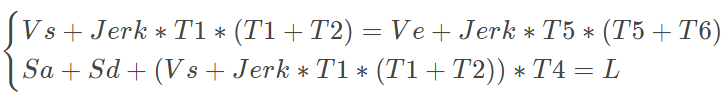 (12)
(12)
其中,Sa和Sd分别由式(6)和(10)计算,并且需要满足以下限制条件:
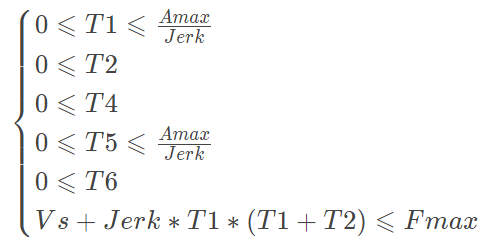 (13)
(13)
这是一个非齐次的非线性的方程组。四个未知数,但是只有两个方程以及一些限制条件。给定初值然后利用迭代法计算也许是求解的一种途径。在设定初值上,可以分情况进行讨论。流程图如下图所示。
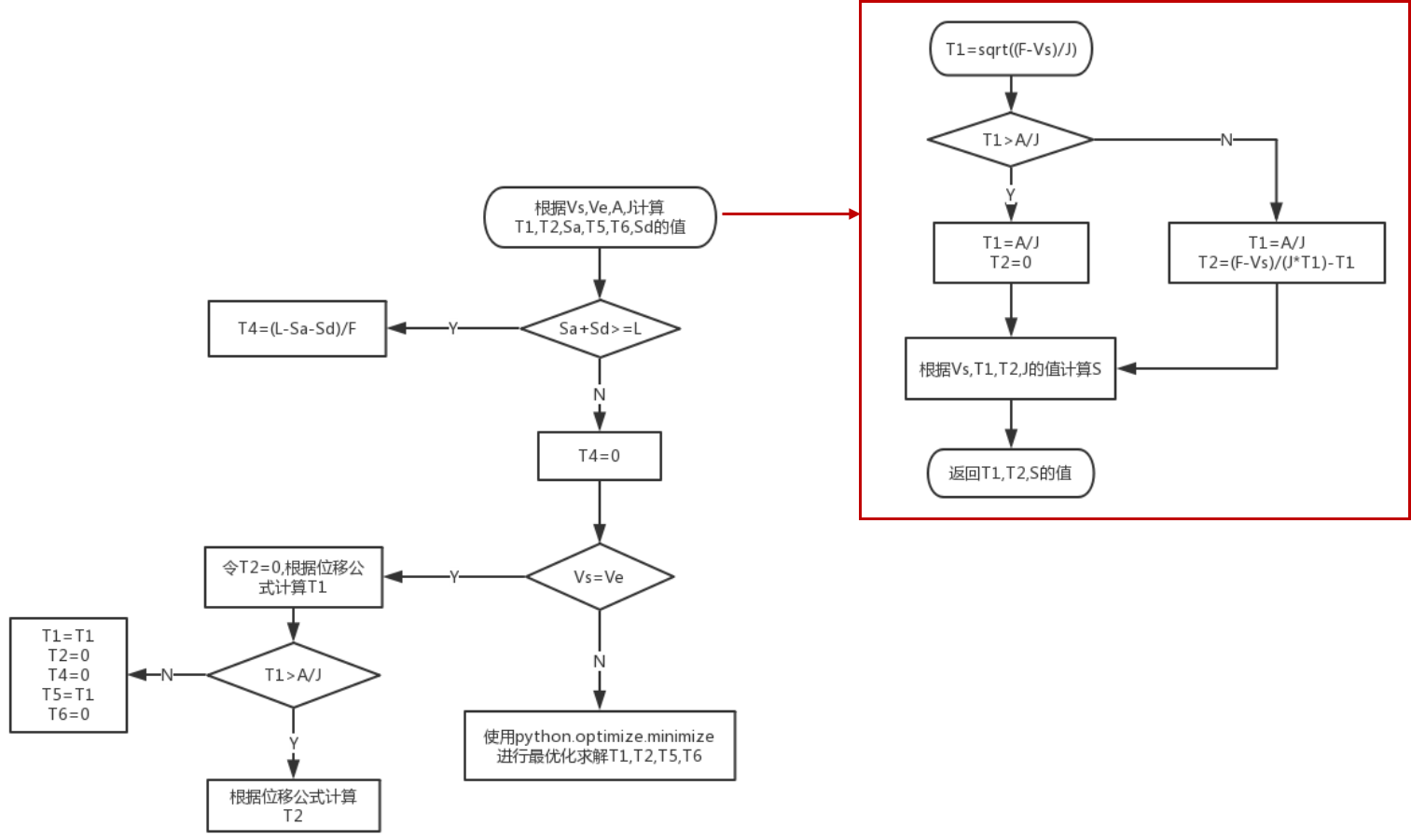
首先使用Vs,Ve,Fmax,Amax,Jerk的值计算T1,T2,T5,T6。计算过程中先假设T2=0,计算速度从Vs达到Fmax所需的时间T1,如果T1<Amax/Jerk,则没有上面的第二个阶段,即加速度匀速的阶段。如果T1>Amax/Jerk,则T1会受到最大加速度的限制,即T1=Amax/Jerk,T2=(Fmax-Vs)/(Jerk*T1)-T1,并且根据T1,T2通过式(6)可以计算出加速阶段的位移Sa。同理可以计算出T5,T6和Sd。
如果Sa+Sd>=L,则说明最大速度可以保持匀速一段时间T4,T4=(L-Sa-Sd)/Fmax
如果Sa+Sd<L,则说明T4=0,且整条速度曲线的峰值达不到最大速度Fmax。因此问题转换为如下的数学问题:
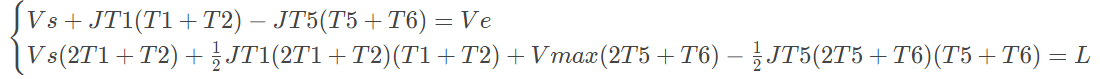 (14)
(14)
求T1,T2,T5,T6。
当Vs=Ve时,T1=T5,T2=T6,则求解式(14)就变成求解式(15)的解:
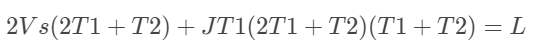 (15)
(15)
也是先假设T2=0,则式(15)是一个关于未知数T1的一元三次方程,且因其判别式大于零,其有唯一解。因此可以求得T1。若T1<Amax/Jerk,则T2=0,若T1>Amax/Jerk,则T1=Amax/Jerk,然后再通过式(15)计算T2。
当Vs≠Ve时,方程组有四个未知数,求不到其唯一解。因此本文中采用的是Python.scipy库中的求最小值的问题来计算T1,T2,T5,T6。即解决如下数学问题:
求T=[T1,T2,T5,T6],使得
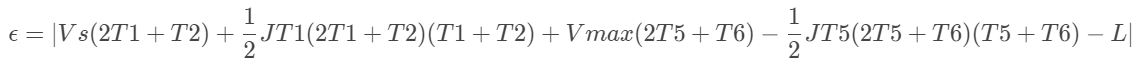 (16)
(16)
值最小,其中,Vmax=Vs+J*T1*(T1+T2)。并满足如下的条件:
 (17)
(17)
下面为这段python代码:
import numpy as np
from scipy.optimize import minimize
import math def motion_profile(args):
vs,J,Fmax,L,t = args
s=lambda x: (vs*t*(2*x[0]+x[1])+J*x[0]*math.pow(t,3)*(2*x[0]+x[1])*(x[0]+x[1])+(vs+J*x[0]*math.pow(t,2)*(x[0]+x[1]))*(2*x[2]+x[3])*t-J*x[2]*math.pow(t,3)*(2*x[2]+x[3])*(x[2]+x[3])-L)**2
return s def cons(args):
Fmax,ve,Amax,J,vs,t = args
cons = ({'type':'ineq',
'fun':lambda x:np.array([Amax/J - x[0]*t,
x[0],
x[1],
x[2],
x[3],
Amax/J - x[2]*t,
ve-vs-J*(x[0]*t)**2 -J*x[0]*t*x[1]*t + J*x[2]*t*x[3]*t + J*(x[2]*t)**2,
Fmax-ve-J*x[2]*math.pow(t,2)*(x[2]+x[3]),
vs + J*(x[0]*t)**2 + J*x[0]*t*x[1]*t - J*x[2]*t*x[3]*t -J*(x[2]*t)**2])})
return cons def optimization(args,args1,x0):
conditions = cons(args1)
res = minimize(motion_profile(args),x0,method='SLSQP',constraints = conditions) time_list = []
time_list.append(res.x[0])
time_list.append(res.x[1])
time_list.append(res.x[2])
time_list.append(res.x[3])
return time_list
整个代码可以见github:
https://github.com/Larissa1990/S-curve-Velocity-Profile
Example1:
Vs=40,Ve=35,Fmax=80,Amax=2000,Jerk=80000,L=5,interpolation_period=0.002
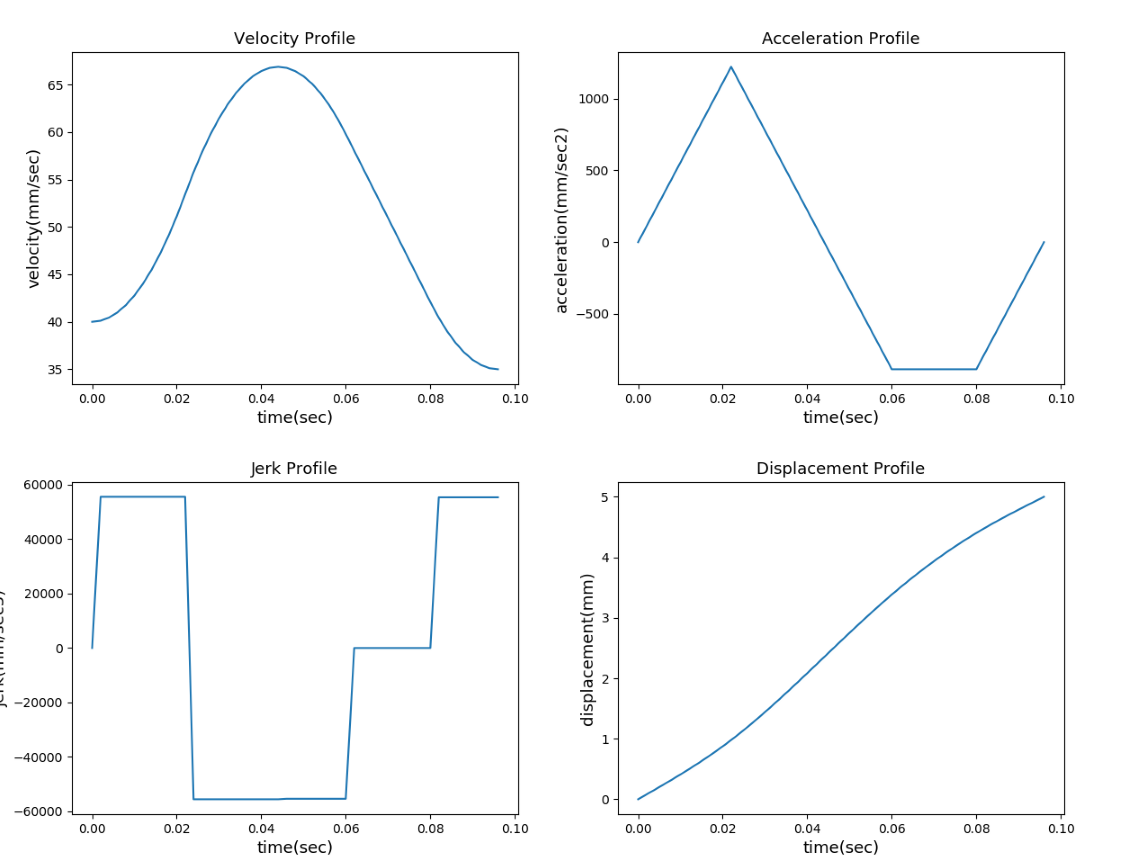
T1=0.022,T2=0,T4=0,T5=0.016,T6=0.02
Example2:
Vs=35,Ve=35,Fmax=80,Amax=2000,Jerk=80000,L=5,interpolation_period=0.002
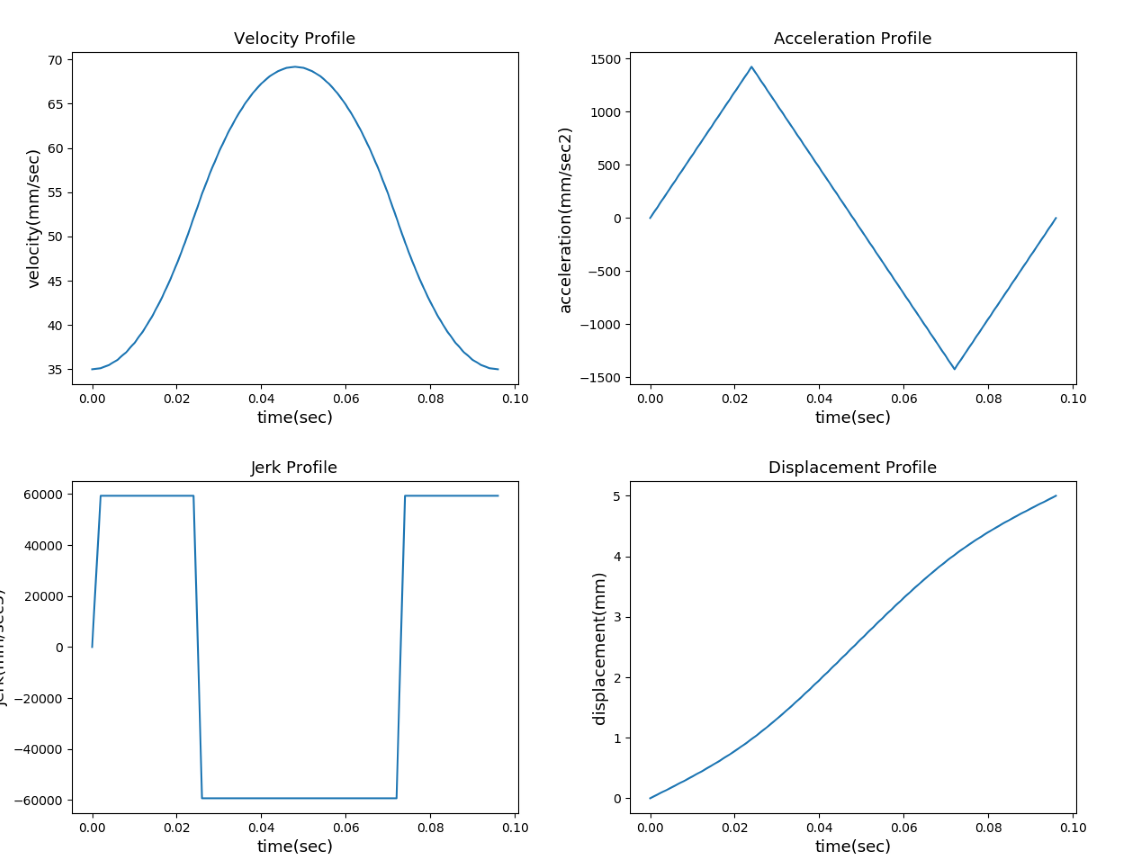
T1=0.024,T2=0,T4=0,T5=0.024,T6=0
3rd S-curve velocity profile的更多相关文章
- an concreate example
Step 1: Creating Parts 1. Split the geometry 2. Create the INLET part. 3. Create the OUTLET part. 4. ...
- ansys 有限元自学手册
李兵.人邮2013.4 实体模型 –> 修正后划分 有限元网格 offset WP 偏移工作平面 模型的建立 将cT轮廓曲线 提取出来输入三维造型软件进行建模的方法,这种方法由于要对 ...
- ICEM相关
1,几何体建模不用讲(可以不学,因为通常是其他软件导入)在初始分块前,建立part,为建立边界条件使用(这是部分的定义最重要的作用,所以你可以按照不同的情况来定义,划分网格只是块的工作),所以对于三维 ...
- Disposable microfluidic devices: fabrication, function, and application Gina S. Fiorini and Daniel T
Disposable microfluidic devices: fabrication, function, and application Gina S. Fiorini and Daniel T ...
- 机器人关节空间轨迹规划--S型速度规划
关节空间 VS 操作空间 关节空间与操作空间轨迹规划流程图如下(上标$i$和$f$分别代表起始位置initial和目标位置final): 在关节空间内进行轨迹规划有如下优点: 在线运算量更小,即无需进 ...
- 机器人中的轨迹规划(Trajectory Planning )
Figure. Several possible path shapes for a single joint 五次多项式曲线(quintic polynomial) $$\theta(t)=a_0+ ...
- 使用yocs_velocity_smoother对机器人速度进行限制
yocs_velocity_smoother是一个速度.加速度限制器,用来防止robot navigation的速度/转速过快,加速度/快减速过大.Bound incoming velocity me ...
- AN2820 Driving bipolar stepper motors using a medium-density STM32F103xx microcontroller
AN2820 Driving bipolar stepper motors using a medium-density STM32F103xx microcontroller Introductio ...
- post processing in CFD
post post Table of Contents 1. Post-processing 1.1. Reverse flow 1.1.1. reasons 1.1.2. solutions 1.2 ...
随机推荐
- C# 反射调用拓展类方法
今天封装Protobuf封包时候遇到一个问题: Protobuf的反序列化方法MergeFrom,是写在扩展类里的:c#拓展类 通过反射获取不到这个方法,就没法使用Type来泛型封装... 然而仔细一 ...
- css中设置背景图片适应屏幕
以body为例 body{ background: url(../img/jld.png) no-repeat center center fixed; -webkit-background-size ...
- linux中yum本地私有仓库安装搭建《全面解析》
目录 一:yum本地仓库安装 1.yum简介 2.yum安装解析 二:yum安装的生命周期 三:yum私有仓库作用与必要性 四:搭建yum私有仓库 本地版本 1.下载必须的软件包 2.创建软件仓库(就 ...
- 安卓开发常见Bug-数据库未加载
安卓的数据库是本地的,所以在项目启动后也就是在onCreat()进行时就要进行数据库加载操作 将数据库加载的操作放在onCreat()中,根据安卓运行生命周期,就实现了数据库的全局化,也就是始终存在于 ...
- C++ 微信多开
应用是如何判断多开 一.通过查找窗口标题或者类名来判断程序是否正在运行. 二.通过互斥对象确定程序是否运行,大多数软件都是使用CreateMutexW 判断多开的. 三.内存映射物理文件,控制多开. ...
- JavaScript通过父节点ID递归生成JSON树
JavaScript通过父节点ID递归生成JSON树: · 实现思路:通过递归实现(第一次递归的时候查询出所有的父节点,然后通过当前父节点id不断地去查询所有子节点,直到递归完毕返回) · 代码示 ...
- 线程池之 newSingleThreadExecutor 介绍
package com.aaa.threaddemo; import java.text.DateFormatSymbols; import java.util.concurrent.Executor ...
- Sweetalert模态对话框与Swiper轮播插件、Bootstrap样式组件、AdminLTE后台管理模板地址
Sweetalert纯JS模态对话框插件地址:http://mishengqiang.com/sweetalert/ AdminLTE后台管理模板系统地址(基于Bootstrap):https://a ...
- SpringBoot的.gitignore文件使用
简介 临时文件,编译的中间文件等不要提交到代码仓库,这时就要设置相应的忽略规则,来忽略这些文件的提交.git提供了一个.gitignore,来自动忽略这些配置文件 配置规则 # 表示此为注释,将被Gi ...
- wget: unable to resolve host address ‘dl.grafana.com’的解决方法
[root@Server-qnrsyp system]# wget --no-check-certificate https://dl.grafana.com/oss/release/grafana_ ...
