「山东省队集训2021 Round 1」 半夜

考虑将 \(X\) 复制一次放到后面再对其长度为 \(n\) 的连续子串和 \(Y\) 求一波 \(\rm{Longest\ Common\ Subsequence}\) 就能得到 \(\Theta(n^3)\) 的分数了

那么设 \(f_{i,j,k}\) 表示 \(X[i\dots j],Y[1\dots k]\) 的 \(LCS\)

考虑如下两个性质：

\[f_{i-1,j,k}>f_{i-1,j-1,k}\Rightarrow f_{i,j,k}>f_{i,j-1,k}
\]

\[f_{i,j,k}>f_{i,j,k-1}\Rightarrow f_{i-1,j,k}>f_{i-1,j,k-1}
\]

下文受篇幅限制只证明第一个：

因为这个 \(\rm{DP}\) 类似于网格图上最大带权游走，那么设两个串的左端点为网格图起始点，右端点为终止点

不难发现两条路径必然存在交点，设 \((i-1,0)\) 到 \((j,k)\) 的 最靠左 路径为 \(C_1\)，而 \((i,0)\) 到 \((j-1,k)\) 的最靠左的最优路径为 \(C_2\)

设两个路径公共部分是 \(C\)，之前是 \(C_1A,C_2A\)，之后的是 \(C_1B,C_2B\)，把已知和结论统统表示出来互相推就行了

那么必然存在 \(\rm{p(j,k),q(j,k)}\) 满足：

\[\rm{f(i,j,k)=f(i,j-1,k)+[i\ge p(k,j)]=f(i,j,k-1)+[i<q(k,j)]}
\]

至此可以得到所有 \(p(n,x)\) 然后使用第一个等号后的式子递推 \(\rm{f(x,x+n-1,n)}\) 即可

考虑如何转移 \(\rm{p,q}\)？

设 \(P=p_{k-1,j},Q=q_{k,j-1}\)（认真注意变量定义）

• \(X_i\ne Y_j\)

  如果 \(P<Q\)，把 \(f_{i,j-1,k},f_{i,j,k-1}\) 的转移结果写出来就能发现 \(p(k,j)=Q,q(k,j)=P\)，因为 \(f_{i,j,k}\ge \max\{f_{i,j-1,k},f_{i,j,k-1}\}\)

  

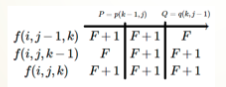
  而对于 \(P\ge Q\) 的情况，仍然是写出来转移的结果得到 \(p_{i,j}=P,q(i,j)=Q\)

  

• \(X_i=Y_j\)

  这里必然会有 \(f_{i,j,k}=f_{i,j-1,k-1}+1\)，那么分开讨论究竟是哪边加了 \(1\)，对转移有贡献的如下：

  如果 \(f_{i,j,k}=f_{i,j-1,k}+1\)，即上次不能转移，但是现在可以，那么必然满足 \(i\ge Q,p(k,j)=Q\)

  如果 \(f_{i,j,k}=f_{i,j,k-1}\)，即提前转移过了，现在不能转移，那么必然满足 \(i\ge P,q(k,j)=p\)

这样就可以了！ 时间复杂度 \(O(n^2)\)

$\texttt{Talk is cheap,Show the Code}$

const int N=2010;
int p[N][N<<1],q[N][N<<1],f[N<<1][N<<1],n,ans;
char x[N<<1],y[N];
signed main(){
	n=read(); scanf("%s%s",x+1,y+1); rep(i,1,n) x[i+n]=x[i];
	rep(i,1,n*2) p[0][i]=i+1; rep(i,1,n*2) q[0][i]=1;
	rep(i,1,n) rep(j,1,(n<<1)){
		int P=p[i-1][j],Q=q[i][j-1];
		if(P>=Q&&x[j]!=y[i]) p[i][j]=P,q[i][j]=Q;
		else p[i][j]=Q,q[i][j]=P;
	}
	rep(i,0,(n<<1)) rep(j,i,(n<<1)) f[i][j]=f[i][j-1]+(i>=p[n][j]);
	rep(i,1,n) ckmax(ans,f[i][i+n-1]); print(ans); return 0;
}
//Use The Time To Enrich This Selfclosing Youth