题解 最长道路tree

题目传送门

题目大意

给出一个\(n\)个点的树，每个点有点权，定义一条链的贡献为该链的点数乘上链上的权值和，求出树上所有链中的权值最大值。

\(n\le 5\times 10^4\)

思路

算是我入边分治的门的一道题吧。。。借鉴了\(\texttt{Miracle}\)巨佬的图、代码以及思路（那不就是转载么？？？（大雾

边分治的大概意思就是说，对于给出的一棵树，我们重新构造成一颗3度树，并且保证我们要求答案的所需性质并不会丢失。然后有一个性质：

于是我们找到重心边分治一下，递归次数就是\(\log n\)级别。于是就能在一个较优的时间复杂度内解决这个问题。

那我们如何对于原树建出一个保留所需信息的3度树呢？有两种方法，第一种就是这样:

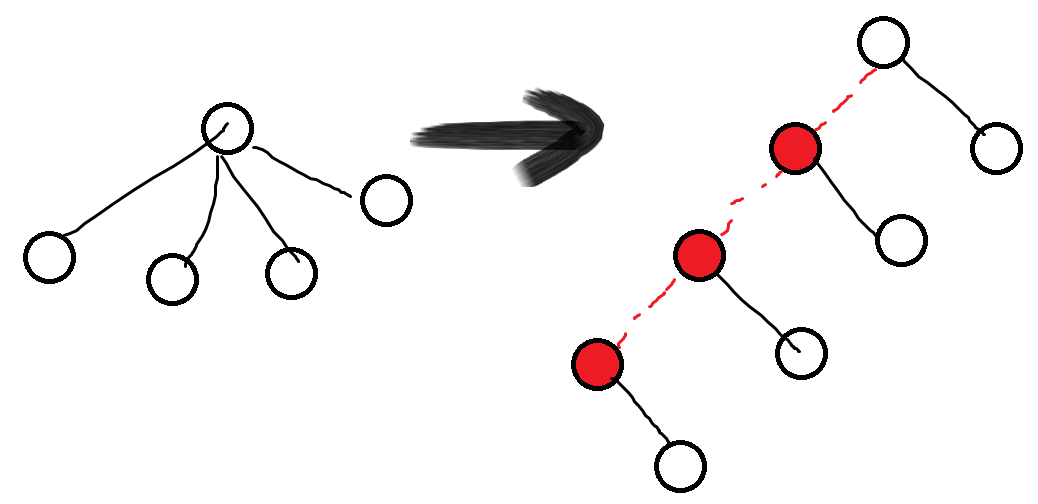
第二种就是建两个虚儿子，然后按奇偶接儿子。

回到这道题，我们显然可以用第一种方法建树，这并不影响答案。我们发现我们边分治似乎对点的问题不是很好解决，但是两个点之间的点的个数等于边的个数+\(1\)，于是我们就可以通过维护边数得到点数。

然后注意虚边的边权为\(0\)就好了，似乎也没有好讲的（手动划掉）。这里讲一个小细节，将两棵子树答案合并的时候可以满足必须要经过这条边，因为不经过的话可以在子树里面找到。不过实现起来的话，强制经过似乎比较好码。（雾

\(\texttt{Code}\)

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define ll long long
#define MAXN 100005

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int n,las[MAXN];
ll ans,val[MAXN];

namespace Graph{
#define fi first
#define se second
#define MP make_pair
#define PII pair<ll,ll>
	int t,ta,tb,top = 1,to[MAXN << 1],wei[MAXN << 1],nxt[MAXN << 1],head[MAXN];
	void Add_Edge (int u,int v,int w){to[++ top] = v,wei[top] = w,nxt[top] = head[u],head[u] = top;}
	void AddEdge (int u,int v,int w){Add_Edge (u,v,w),Add_Edge (v,u,w);}
	bool vis[MAXN << 1];
	int siz[MAXN],lim,ed,Siz;//ed表示当前重心边
	void dfs (int u,int fa){
		siz[u] = 1;
		for (Int i = head[u],v;i;i = nxt[i]){
			if (vis[i] || (v = to[i]) == fa) continue;
			dfs (v,u),siz[u] += siz[v];
			int tmp = max (siz[v],Siz - siz[v]);
			if (tmp < lim) lim = tmp,ed = i;
		}
	}
	PII A[MAXN],B[MAXN],*f;
	void dfs (int u,int fa,ll minn,ll dis){
		minn = min (minn,val[u]),f[++ t] = MP (minn,dis);
		for (Int i = head[u],v;i;i = nxt[i]){
			if (vis[i] || (v = to[i]) == fa) continue;
			dfs (v,u,minn,dis + wei[i]);
		}
	}
	void Solve (int u,int S){//S表示当前子树大小
		if (S <= 1) return ;
		lim = Siz = S,dfs (u,0),vis[ed] = vis[ed ^ 1] = 1;
		t = 0,f = A,dfs (to[ed],0,1e9,0),ta = t;
		t = 0,f = B,dfs (to[ed ^ 1],0,1e9,0),tb = t;
		sort (A + 1,A + ta + 1),sort (B + 1,B + tb + 1);
		int j = tb;ll mx = 0,l = wei[ed];
		for (Int i = ta;i;-- i){
			while (j > 1 && B[j].fi >= A[i].fi) mx = max (mx,B[j --].se);
			if (j < tb) ans = max (ans,(A[i].se + mx + 1 + l) * A[i].fi);
		}
		j = ta,mx = 0;
		for (Int i = tb;i;-- i){
			while (j > 1 && A[j].fi >= B[i].fi) mx = max (mx,A[j --].se);
			if (j < ta) ans = max (ans,(B[i].se + mx + 1 + l) * B[i].fi);
		}
		int tx = to[ed],ty = to[ed ^ 1];
		Solve (tx,siz[tx]),Solve (ty,S - siz[tx]);
	}
}

int top = 1,cnt,to[MAXN << 1],nxt[MAXN << 1],head[MAXN];
void Add_Edge (int u,int v){to[++ top] = v,nxt[top] = head[u],head[u] = top;}

void dfs (int u,int fa){
	for (Int i = head[u],v;i;i = nxt[i]){
		if ((v = to[i]) == fa) continue;dfs (v,u);
		if (!las[u]) Graph::AddEdge (u,v,1),las[u] = u;
		else ++ cnt,Graph::AddEdge (las[u],cnt,0),Graph::AddEdge (las[u] = cnt,v,1),val[cnt] = val[u];
	}
}

signed main(){
	read (n),cnt = n;
	for (Int i = 1;i <= n;++ i) read (val[i]);
	for (Int i = 2,u,v;i <= n;++ i) read (u,v),Add_Edge (u,v),Add_Edge (v,u);
	dfs (1,0),Graph::Solve (1,cnt);
	write (ans),putchar ('\n');
	return 0;
}