练习推导一个最简单的BP神经网络训练过程【个人作业/数学推导】

写在前面

  各式资料中关于BP神经网络的讲解已经足够全面详尽，故不在此过多赘述。本文重点在于由一个“最简单”的神经网络练习推导其训练过程，和大家一起在练习中一起更好理解神经网络训练过程。

一、BP神经网络

1.1 简介

  BP网络（Back-Propagation Network） 是1986年被提出的，是一种按误差逆向传播算法训练的

  多层前馈网络，是目前应用最广泛的神经网络模型之一，用于函数逼近、模型识别分类、数据压缩和时间序列预测等。

  一个典型的BP网络应该包括三层:输入层、隐藏层和输出层。各层之间全连接，同层之间无连接。隐藏层可以有很多层。

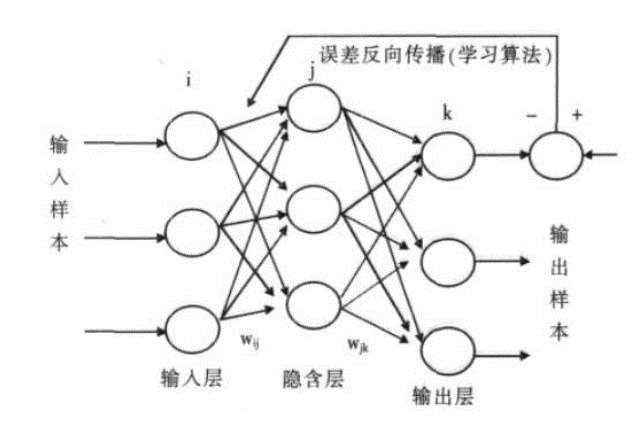
Fig 1 数字图像与对应矩阵图示

1.2 训练(学习)过程

  每一次迭代(Interation)意味着使用一批(Batch)数据对模型进行一次更新过程，被称为“一次训练”，包含一个正向过程和一个反向过程。

具体过程可以概括为如下过程：

1. 准备样本信息(数据&标签)、定义神经网络(结构、初始化参数、选取激活函数等)
2. 将样本输入，正向计算各节点函数输出
3. 计算损失函数
4. 求损失函数对各权重的偏导数，采用适当方法进行反向过程优化
5. 重复2~4直至达到停止条件

  以下训练将使用均值平方差（Mean Squared Error， MSE）作为损失函数，sigmoid函数作为激活函数、梯度下降法作为优化权重方法进行推导

二、实例推导练习作业

2.1 准备工作

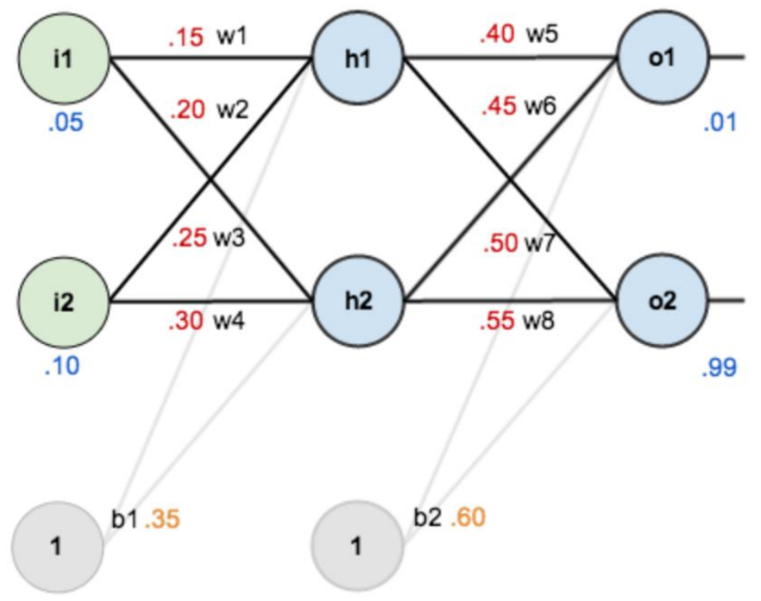
Fig 2 所定义神经网络、初始化参数、样本信息等

1. 第一层是输入层，包含两个神经元： i1， i2 和偏置b1
2. 第二层是隐藏层，包含两个神经元： h1， h2 和偏置项b2
3. 第三层是输出： o1， o2
4. 每条线上标的 wi 是层与层之间连接的权重
5. 激活函数是 sigmod 函数
6. 我们用 z 表示某神经元的加权输入和，用 a 表示某神经元的输出

2.2 第一次正向过程【个人推导】

  根据上述信息，我们可以得到另一种表达一次迭代的“环形”过程的图示如下：

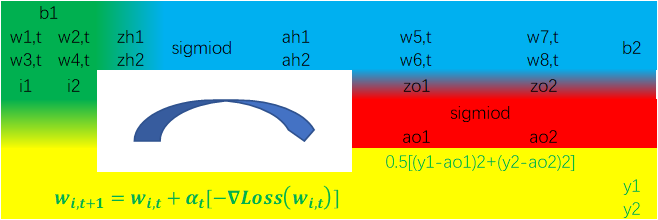
Fig 3 bp神经网络数量关系“环”图示


  我们做一次正向过程(由于需多次迭代，因此我们将第一次正向过程标记为t=0)，得各项数值如下：

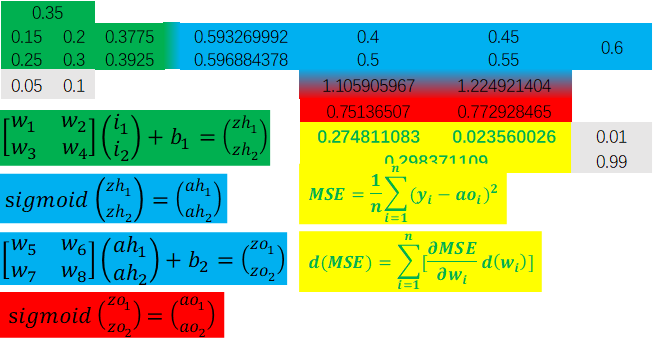
Fig 4 初始数值“环”图示(附函数关系表达式)


  由此我们可得损失函数值为MSE=0.298371109，假设这超出了我们对损失值的要求，那么我们就需要对各个权重(wi,t=0)进行更新， 作为t=1的初始权重。

2.3 推导计算∂/∂wi【个人推导】

2.3.1 均值平方差损失函数的全微分推导

\(dMSE=\frac{\partial MSE}{\partial ao_{1}}dao_{1}+\frac{\partial MSE}{\partial ao_{2}}dao_{2}\)

\({\color{white}{dMSE}}=\frac{\partial MSE}{\partial ao_{1}}\frac{\partial ao_{1}}{\partial zo_{1}} dzo_{1}
+\frac{\partial MSE}{\partial ao_{2}}\frac{\partial ao_{2}}{\partial zo_{2}} dzo_{2}\)

\({\color{white}{dMSE}}=\frac{\partial MSE}{\partial ao_{1}}\frac{\partial ao_{1}}{\partial zo_{1}}\left ( \frac{\partial zo_{1}}{\partial ah_{1}}dah_{1}
+\frac{\partial zo_{1}}{\partial ah_{2}}dah_{2}
+
\frac{\partial zo_{1}}{\partial w\omega _{5}}d\omega _{5}
+\frac{\partial zo_{1}}{\partial w\omega _{6}}d\omega _{6}
\right )\)

\({\color{white}{dMSE=}}+\frac{\partial MSE}{\partial ao_{2}}\frac{\partial ao_{2}}{\partial zo_{2}}\left ( \frac{\partial zo_{2}}{\partial ah_{1}}dah_{1}
+\frac{\partial zo_{2}}{\partial ah_{2}}dah_{2}
+
\frac{\partial zo_{2}}{\partial w\omega _{7}}d\omega _{7}
+\frac{\partial zo_{2}}{\partial w\omega _{8}}d\omega _{8}
\right )\)

\({\color{white}{dMSE}}=\frac{\partial MSE}{\partial ao_{1}}\frac{\partial ao_{1}}{\partial zo_{1}}\left ( \frac{\partial zo_{1}}{\partial ah_{1}}\frac{\partial ah_{1}}{\partial zh_{1}}dzh_{1}
+\frac{\partial zo_{1}}{\partial ah_{2}}\frac{\partial ah_{2}}{\partial zh_{2}}dzh_{2}
+
\frac{\partial zo_{1}}{\partial w\omega _{5}}d\omega _{5}
+\frac{\partial zo_{1}}{\partial w\omega _{6}}d\omega _{6}
\right )\)

\({\color{white}{dMSE=}}+\frac{\partial MSE}{\partial ao_{2}}\frac{\partial ao_{2}}{\partial zo_{2}}\left ( \frac{\partial zo_{2}}{\partial ah_{1}}\frac{\partial ah_{1}}{\partial zh_{1}}dzh_{1}
+\frac{\partial zo_{2}}{\partial ah_{2}}\frac{\partial ah_{2}}{\partial zh_{2}}dzh_{2}
+
\frac{\partial zo_{2}}{\partial w\omega _{7}}d\omega _{7}
+\frac{\partial zo_{2}}{\partial w\omega _{8}}d\omega _{8}
\right )\)

\({\color{white}{dMSE}}=\frac{\partial MSE}{\partial ao_{1}}\frac{\partial ao_{1}}{\partial zo_{1}}\left [ \frac{\partial zo_{1}}{\partial ah_{1}}\frac{\partial ah_{1}}{\partial zh_{1}}\left ( \frac{\partial zh_{1}}{\partial \omega _{1}}d\omega _{1}+\frac{\partial zh_{1}}{\partial \omega _{2}}d\omega _{2} \right )
+\frac{\partial zo_{1}}{\partial ah_{2}}\frac{\partial ah_{2}}{\partial zh_{2}}\left ( \frac{\partial zh_{2}}{\partial \omega _{3}}d\omega _{3}+\frac{\partial zh_{2}}{\partial \omega _{4}}d\omega _{4} \right )
+
\frac{\partial zo_{1}}{\partial w\omega _{5}}d\omega _{5}
+\frac{\partial zo_{1}}{\partial w\omega _{6}}d\omega _{6}
\right ]\)

\({\color{white}{dMSE=}}+\frac{\partial MSE}{\partial ao_{2}}\frac{\partial ao_{2}}{\partial zo_{2}}\left [ \frac{\partial zo_{2}}{\partial ah_{1}}\frac{\partial ah_{1}}{\partial zh_{1}}\left ( \frac{\partial zh_{1}}{\partial \omega _{1}}d\omega _{1}+\frac{\partial zh_{1}}{\partial \omega _{2}}d\omega _{2} \right )
+\frac{\partial zo_{2}}{\partial ah_{2}}\frac{\partial ah_{2}}{\partial zh_{2}}\left ( \frac{\partial zh_{2}}{\partial \omega _{3}}d\omega _{3}+\frac{\partial zh_{2}}{\partial \omega _{4}}d\omega _{4} \right )
+
\frac{\partial zo_{2}}{\partial w\omega _{7}}d\omega _{7}
+\frac{\partial zo_{2}}{\partial w\omega _{8}}d\omega _{8}
\right ]\)

2.3.2 这一次代入训练实例的数值和各数量名

\(dMSE=\frac{\partial \frac{1}{2}\left ( y_{1}-ao_{1} \right )^2}{\partial ao_{1}}dao_{1}+\frac{\partial \frac{1}{2}\left ( y_{2}-ao_{2} \right )^2}{\partial ao_{2}}dao_{2}\)

\({\color{white}{dMSE}}=-\left( y_{1}-ao_{1} \right )\frac{\partial ao_{1}}{\partial zo_{1}}dzo_{1}-\left( y_{2}-ao_{2} \right )\frac{\partial ao_{2}}{\partial zo_{2}}dzo_{2}\)

\({\color{white}{dMSE}}=-\left( y_{1}-ao_{1} \right )ao_{1}\left( 1-ao_{1} \right )\left ( \frac{\partial zo_{1}}{\partial ah_{1}}dah_{1}+\frac{\partial zo_{1}}{\partial ah_{2}}dah_{2}+\frac{\partial zo_{1}}{\partial \omega _{5}}d\omega _{5}+\frac{\partial zo_{1}}{\partial \omega _{6}}d\omega _{6} \right )\)

\({\color{white}{dMSE=}}-\left( y_{2}-ao_{2} \right )ao_{2}\left( 1-ao_{2} \right )\left ( \frac{\partial zo_{2}}{\partial ah_{1}}dah_{1}+\frac{\partial zo_{2}}{\partial ah_{2}}dah_{2}+\frac{\partial zo_{2}}{\partial \omega _{7}}d\omega _{7}+\frac{\partial zo_{2}}{\partial \omega _{8}}d\omega _{8} \right )\)

\({\color{white}{dMSE}}=-\left( y_{1}-ao_{1} \right )ao_{1}\left( 1-ao_{1} \right )\left ( \omega_{5}\frac{\partial ah_{1}}{\partial zh_{1}}dzh_{1}+\omega_{6}\frac{\partial ah_{2}}{\partial zh_{2}}dzh_{2}+ah_{1}d\omega _{5}+ah_{2}d\omega _{6} \right )\)

\({\color{white}{dMSE=}}-\left( y_{2}-ao_{2} \right )ao_{2}\left( 1-ao_{2} \right )\left ( \omega_{7}\frac{\partial ah_{1}}{\partial zh_{1}}dzh_{1}+\omega_{8}\frac{\partial ah_{2}}{\partial zh_{2}}dzh_{2}+ah_{1}d\omega _{7}+ah_{2}d\omega _{8} \right )\)

\({\color{white}{dMSE}}=-\left ( y_{1}-ao_{1} \right )ao_{1}\left( 1-ao_{1} \right )\left [ \omega_{5}\cdot ah_{1}\left ( 1- ah_{1} \right )\left (\frac{\partial zh_{1}}{\partial \omega_{1}}\omega_{1}+\frac{\partial zh_{1}}{\partial \omega_{2}}\omega_{2} \right )
+\omega_{6}\cdot ah_{2}\left ( 1- ah_{2} \right )\left (\frac{\partial zh_{2}}{\partial \omega_{3}}\omega_{3}+\frac{\partial zh_{2}}{\partial \omega_{4}}\omega_{4} \right )+ah_{1}d\omega _{5}+ah_{2}d\omega _{6} \right ]\)

\({\color{white}{dMSE=}}-\left ( y_{2}-ao_{2} \right )ao_{2}\left( 1-ao_{2} \right )\left [ \omega_{7}\cdot ah_{1}\left ( 1- ah_{1} \right )\left (\frac{\partial zh_{1}}{\partial \omega_{1}}\omega_{1}+\frac{\partial zh_{1}}{\partial \omega_{2}}\omega_{2} \right )
+\omega_{8}\cdot ah_{2}\left ( 1- ah_{2} \right )\left (\frac{\partial zh_{2}}{\partial \omega_{3}}\omega_{3}+\frac{\partial zh_{2}}{\partial \omega_{4}}\omega_{4} \right )+ah_{1}d\omega _{7}+ah_{2}d\omega _{8} \right ]\)

\({\color{white}{dMSE}}=-\left ( y_{1}-ao_{1} \right )ao_{1}\left( 1-ao_{1} \right )\left[ \omega_{5} \cdot ah_{1}\left ( 1-ah_{1} \right )\left ( {\color{green}{i_{1}d\omega_{1}}}+{\color{green}{i_{2}d\omega_{2}}} \right )
+\omega_{6} \cdot ah_{2}\left ( 1-ah_{2} \right )\left ( {\color{green}{i_{1}d\omega_{3}}}+{\color{green}{i_{2}d\omega_{4}}} \right )
+{\color{blue}{ah_{1}d\omega_{5}}}+{\color{blue}{ah_{2}d\omega_{6}}}\right ]\)

\({\color{white}{dMSE=}}-\left ( y_{2}-ao_{2} \right )ao_{2}\left( 1-ao_{2} \right )\left[ \omega_{7} \cdot ah_{1}\left ( 1-ah_{1} \right )\left ( {\color{green}{i_{1}d\omega_{1}}}+{\color{green}{i_{2}d\omega_{2}}} \right )
+\omega_{8} \cdot ah_{2}\left ( 1-ah_{2} \right )\left ( {\color{green}{i_{1}d\omega_{3}}}+{\color{green}{i_{2}d\omega_{4}}} \right )
+{\color{blue}{ah_{1}d\omega_{7}}}+{\color{blue}{ah_{2}d\omega_{8}}}\right ]\)

2.3.3 由此我们得到∂/∂wi的表达式

\(\frac {\partial MSE}{\partial \omega_{1}}=-\left [ \left( y_{1}-ao_{1} \right )ao_{1}\left ( 1-ao_{1} \right )\cdot \omega_{5}\cdot ah_{1}\left ( 1-ah_{1} \right )+\left( y_{2}-ao_{2} \right )ao_{2}\left ( 1-ao_{2} \right )\cdot \omega_{7}\cdot ah_{1}\left ( 1-ah_{1} \right ) \right ]\cdot i_{1}\)

\(\frac {\partial MSE}{\partial \omega_{2}}=-\left [ \left( y_{1}-ao_{1} \right )ao_{1}\left ( 1-ao_{1} \right )\cdot \omega_{5}\cdot ah_{1}\left ( 1-ah_{1} \right )+\left( y_{2}-ao_{2} \right )ao_{2}\left ( 1-ao_{2} \right )\cdot \omega_{7}\cdot ah_{1}\left ( 1-ah_{1} \right ) \right ]\cdot i_{2}\)

\(\frac {\partial MSE}{\partial \omega_{3}}=-\left [ \left( y_{1}-ao_{1} \right )ao_{1}\left ( 1-ao_{1} \right )\cdot \omega_{6}\cdot ah_{2}\left ( 1-ah_{2} \right )+\left( y_{2}-ao_{2} \right )ao_{2}\left ( 1-ao_{2} \right )\cdot \omega_{8}\cdot ah_{2}\left ( 1-ah_{2} \right ) \right ]\cdot i_{1}\)

\(\frac {\partial MSE}{\partial \omega_{4}}=-\left [ \left( y_{1}-ao_{1} \right )ao_{1}\left ( 1-ao_{1} \right )\cdot \omega_{6}\cdot ah_{2}\left ( 1-ah_{2} \right )+\left( y_{2}-ao_{2} \right )ao_{2}\left ( 1-ao_{2} \right )\cdot \omega_{8}\cdot ah_{2}\left ( 1-ah_{2} \right ) \right ]\cdot i_{2}\)

\(\frac {\partial MSE}{\partial \omega_{5}}=-\left( y_{1}-ao_{1} \right )ao_{1}\left ( 1-ao_{1} \right )\cdot ah_{1}\)

\(\frac {\partial MSE}{\partial \omega_{6}}=-\left( y_{1}-ao_{1} \right )ao_{1}\left ( 1-ao_{1} \right )\cdot ah_{2}\)

\(\frac {\partial MSE}{\partial \omega_{7}}=-\left( y_{2}-ao_{2} \right )ao_{2}\left ( 1-ao_{2} \right )\cdot ah_{1}\)

\(\frac {\partial MSE}{\partial \omega_{8}}=-\left( y_{2}-ao_{2} \right )ao_{2}\left ( 1-ao_{2} \right )\cdot ah_{2}\)


  当然如果你喜欢用矩阵表示也可以：

(P.S. Markdown编辑器承受不住如此“巨大”的矩阵算式而崩溃，我只好转成svg图片贴上了，见谅~)

2.4 根据∂/∂wi梯度下降法优化wi【个人推导】

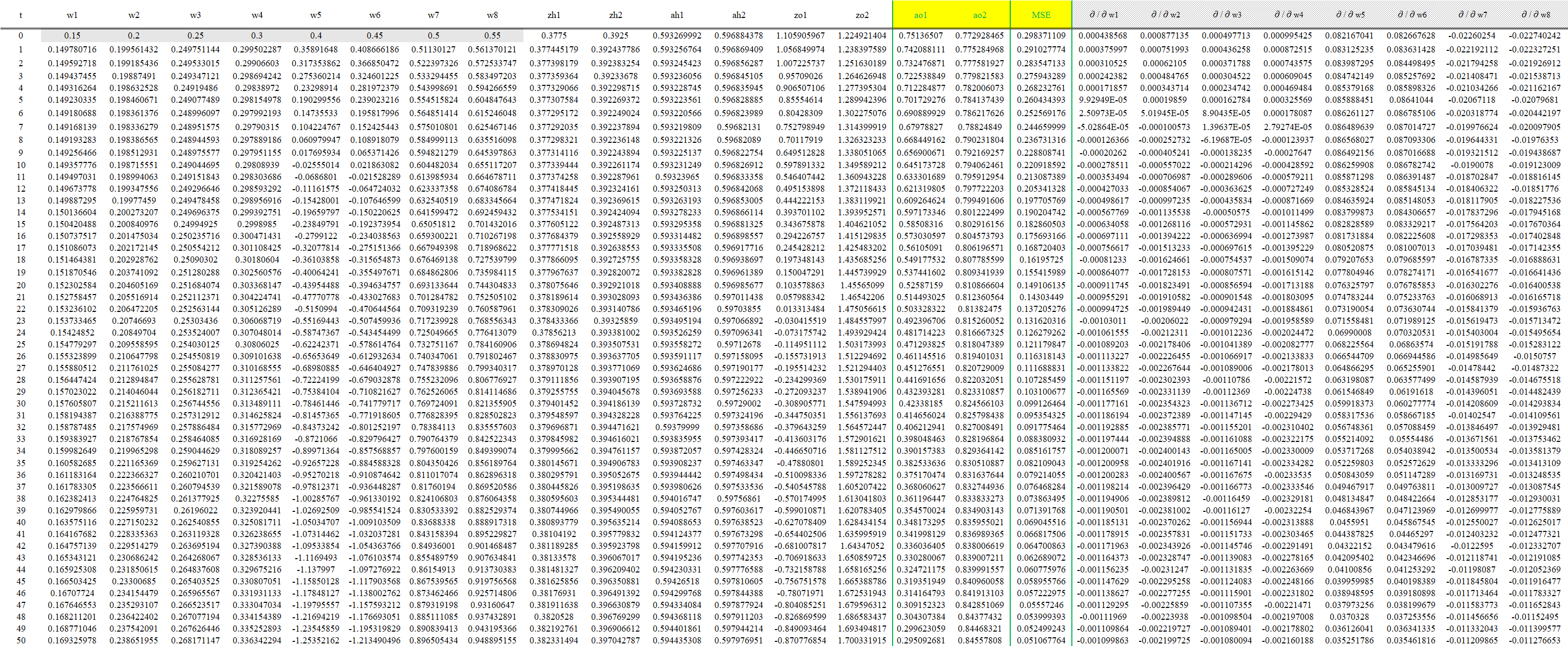
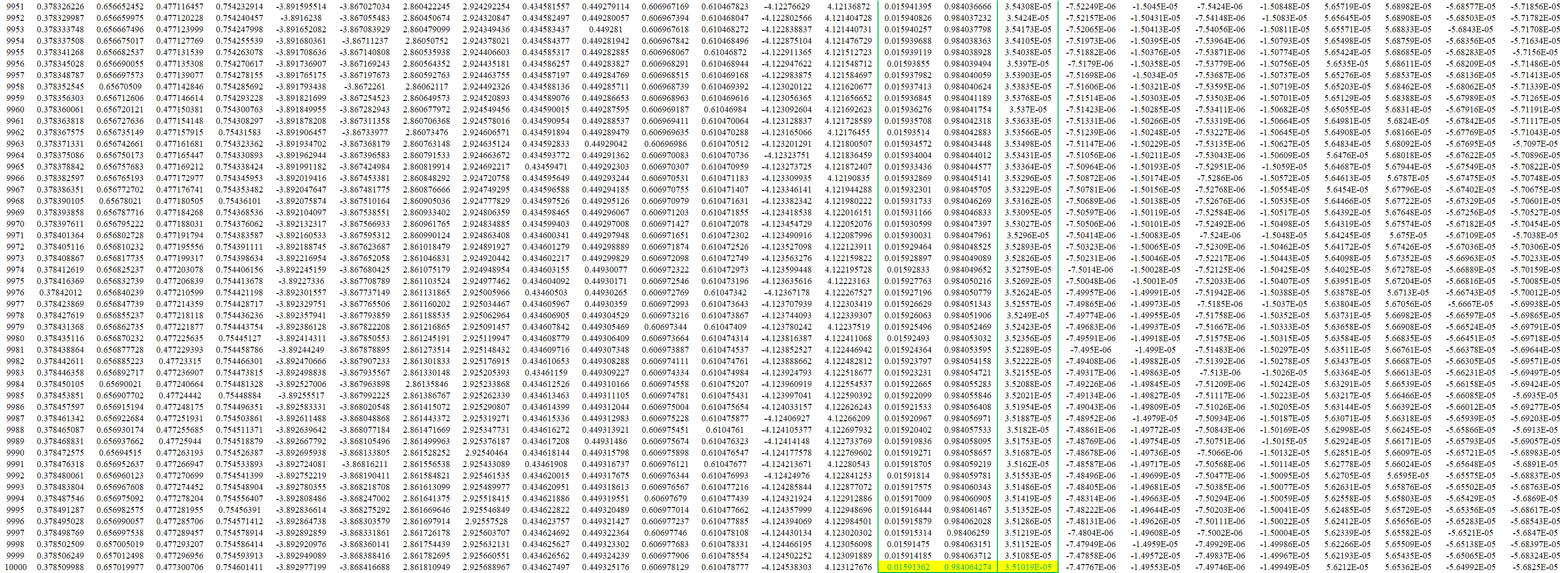
  根据梯度下降法\({\color{purple}{\omega_{i,t+1}=\omega_{i,t}+\alpha_{t}\left [ -\triangledown Loss(\omega_{i,t}) \right ]}}\)，设置学习率α=0.5，计算出wi,t+1，然后重新进行下一次正向过程。(可以将该过程在Excel中轻易实现，下表中为迭代数据截取)

  可以看到，经过10001次迭代之后MSE(t=10001)=3.51019E-05已经足够小，可以停止迭代完成1代训练。

………………………………………………………………………………………………………………………………………………

sigmoid函数求导Tips(for于初级选手)

\(\because {\color{blue}{\frac{1}{1+e^{-x}}}}=\frac{1}{1+\frac{1}{e^{x}}}=\frac{e^{x}}{e^{x}+1}={\color{blue}{1-\frac{1}{1+e^{x}}}}\)

\(\therefore \frac{d\left( {\color{red}{\frac{1}{1+e^{-x}}}} \right )}{dx}=
d\left( 1-\frac{1}{e^{x}+1} \right )\frac{1}{dx}\)

\({\color{white}{\therefore \frac{d\left( \frac{1}{1+e^{-x}} \right )}{dx}}}=
(-1)\times (-1)(e^{x}+1)^{-2}d(e^{x}+1)\frac{1}{dx}\)

\({\color{white}{\therefore \frac{d\left( \frac{1}{1+e^{-x}} \right )}{dx}}}=
\frac{e^{x}}{(e^{x}+1)^2}\frac{1}{dx}=-\left[ \frac{1}{e^x+1}-\frac{1}{(e^x+1)^2} \right ]\frac{1}{dx}\)

\({\color{white}{\therefore \frac{d\left( \frac{1}{1+e^{-x}} \right )}{dx}}}=
\frac{1}{1+e^{x}}\left [ 1-\frac{1}{e^x+1} \right ]\frac{1}{dx}\)

\({\color{white}{\therefore \frac{d\left( \frac{1}{1+e^{-x}} \right )}{dx}}}=
\left ( {\color{red}{1-\frac{1}{1+e^{-x}}}} \right )\left [ {\color{red}{\frac{1}{1+e^x}}} \right ]\frac{1}{dx}\)