Acwing_蓝桥_递归

一.关于由数据范围反推算法复杂度及其算法

关于输入输出：问题规模小于10⁵：cin，scanf都差不多，但是要是大于10⁵推荐使用scanf和printf。

二.关于递归

1.定义

自己调用自己

2.注意事项：

• 判断递归结束的边界
• 少调用局部变量，会占用很大的内存
• 要怎么调用自身

3.每个递归都可以转化成递归搜索树

例如计算斐波那契数列可以转化成如下（这里不讨论剪枝，也就是不把重复的剪掉）

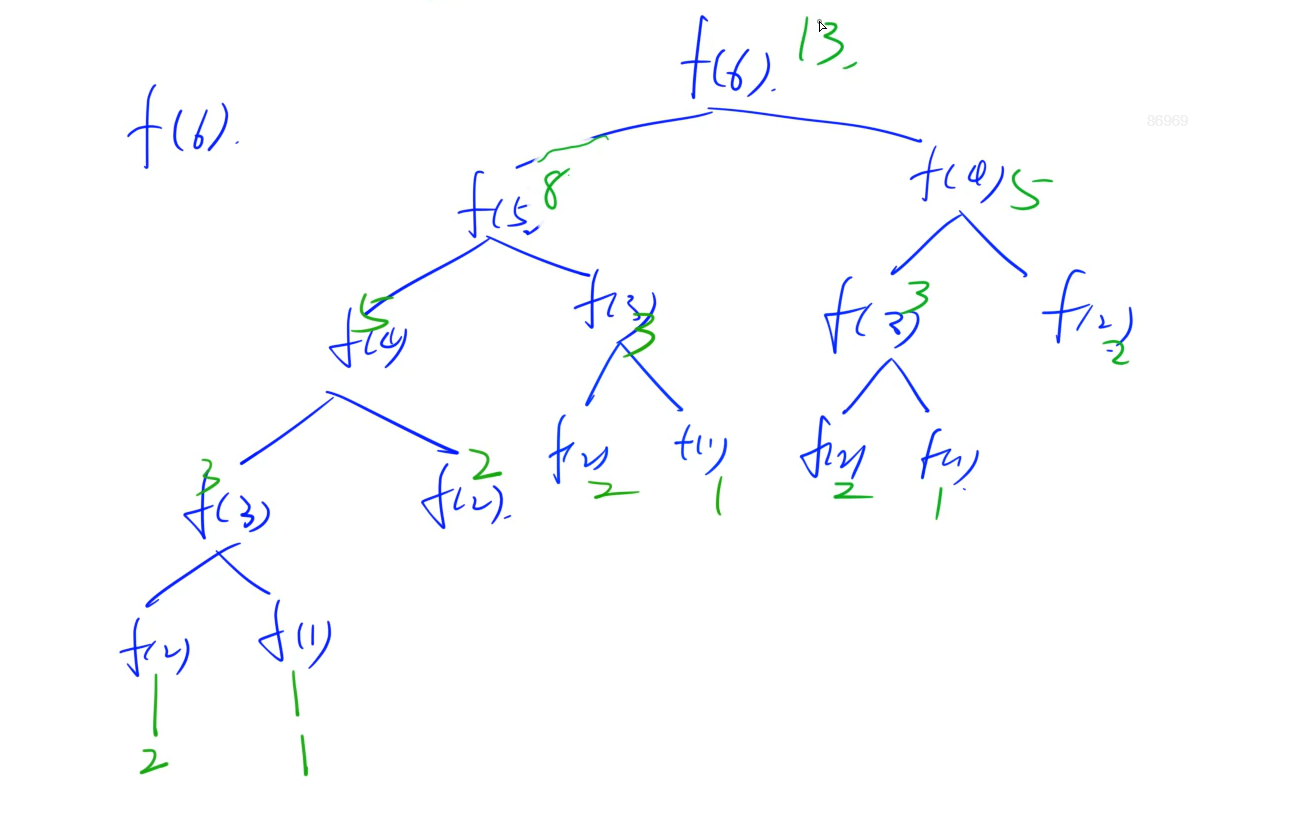
三.递归练习

1.递归实现指数型枚举

https://www.acwing.com/problem/content/94/

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;

const int N = 16;

int n;
int st[N];//表示状态：0表示还不考虑，1表示选，2表示不选

void dfs(int u)
{
    if(u > n) // 终止条件
    {
        for(int i = 1; i <= n; i++)
            if(st[i] == 1) printf("%d ", i);
        puts("");
        return;
    }

    st[u] = 1;
    dfs(u + 1);
    st[u] = 0;//回溯，要恢复原来的状态

    st[u] = 2;
    dfs(u + 1);
    st[u] = 0;
}

int main()
{
    scanf("%d", &n);
    dfs(1);
    return 0;
}

2.递归实现排列型枚举

https://www.acwing.com/problem/content/96/

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 10;
int st[N];
bool used[N];
int n;

void bfs(int u)
{
    if (u > n)
    {
        for (int i = 1; i <= n; i++) printf("%d ", st[i]);
        printf("\n");
        return;
    }
    for (int i = 1; i <= n; i++)
    {
        if (!used[i]) //表示i没有被用过
        {
            used[i] = true;
            st[u] = i;
            bfs(u+1);
            st[u] = 0;
            used[i] = false;
        }
    }
}

int main()
{
    scanf("%d", &n);
    bfs(1);
    return 0;
}

关于上面递归算法的时间复杂度分析：

第一层中的基本操作是for循环进行深搜，遍历为O(n),然后递归中有n个这样的函数，也就是n个分支。第二层也是一个for循环，然后循环中有n-1个分支，时间复杂度是O(n(n-1))。第三层就是O(n(n-1)(n-2)),以此类推，最后一层是的时间复杂度是O(nn!)。所以总的时间复杂度是O(n(1+n+n(n-1)+...+n!)),该循环是大于O（n!）的，经过放缩法可以证明是小于O（3n！）。所以最终时间复杂度为O（n*n!）

3.递归实现组合型枚举

https://www.acwing.com/problem/content/95/

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;

const int N = 30;
int n,m;
int st[N];
bool path[N];

void dfs(int u,int t)
{
    if(u == m)
    {
        for(int i = 0 ; i < m ; i ++ ) printf("%d ", st[i]);
        printf("\n");
        return;
    }
    for(int i = t; i <= n ; i++)
    {
        if(u==0&&i + m - 1 > n ) break;
        if(!path[i])
        {
            st[u] = i;
            path[i] = true;
            dfs(u+1,i+1);
            if(u)path[i] = false;
        }
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    dfs(0,1);
    return 0;
}