【机器学习】主成分分析法 PCA （I）

主成分分析算法是最常见的降维算法，在PCA中，我们要做的是找到一个方向向量，然后我们把所有的数都投影到该向量上，使得投影的误差尽可能的小。投影误差就是特征向量到投影向量之间所需要移动的距离。

PCA的目的是找到一个最下投影误差平方的低维向量，对原有数据进行投影，从而达到降维的目的。

下面给出主成分分析算法的描述：

问题是要将n维数据降至k维，目标是找出向量μ（k），使得投影误差最小。

主成分分析算法与线性回归类似，但区别是投影方式的不同。

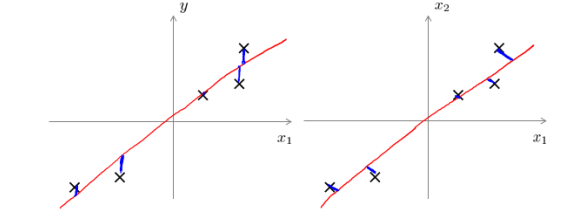
如图所示，的左边的图是垂直与x轴进行的投影，这是线性回归的误差，而右边的投影方法是垂直与回归直线进行投影。PCA将n个特征降维到k个，可以用来压缩数据，也可以用来使得数据可视化。‘

PCA技术最大的优点是对数据进行降维，在起到压缩数据的同时，最大程度的保持了原始数据。

而且它是完全无参数限制，在计算过程中，完全不需要人为的设定多余参数，对经验模型的计算进行干预。

如何通过PCA算法进行降维？

PCA算法减少n维到k维：

step 1: 均值归一化，我们需要计算出所有向量的均值，然后令x j = x j - μ j。如果特征是在不同的数量级上，我们还需要除以标准差δ ².

step 2：计算协方差矩阵∑：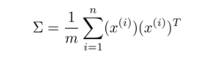

step 3：计算协方差矩阵的特征向量。

在octave（MATLAB）中 我们可以通过利用 ”奇异值分解“ 的方法来求解[U,S,V] = svd(sigma).

MATLAB中自带了进行主成分分析的函数，在命令行中输入help pca可以查到该函数的以下几种用法：

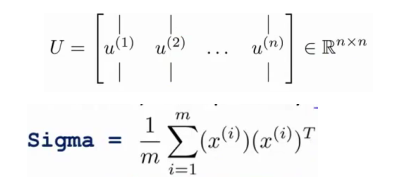
coeff = pca(X)
coeff = pca(X,Name,Value)
[coeff,score,latent] = pca(___)
[coeff,score,latent,tsquared] = pca(___)
[coeff,score,latent,tsquared,explained,mu] = pca(___)

　　

其中，coeff为为X所对应的协方差矩阵的特征值向量，latent为特征值组成的向量，score是原X矩阵在主成分空间的表示，tsquared表示霍特林T方统计值。

例如 对二维数组X = [1 2 3 4 5;1 3 2 5 4];进行降维

coeff, ~, latent] = pca(X');
[~,i] = max(latent);
P = coeff(:,i);
Y = P'*X;