C++版 - Leetcode 69. Sqrt(x) 解题报告【C库函数sqrt(x)模拟-求平方根】

69. Sqrt(x)

Total Accepted: 93296 Total Submissions: 368340 Difficulty: Medium

提交网址： https://leetcode.com/problems/sqrtx/

Implement int sqrt(int x).

Compute and return the square root of x.

分析：

解法1：牛顿迭代法(牛顿切线法)

Newton's Method(牛顿切线法)是由艾萨克·牛顿在《流数法》(Method of Fluxions，1671年完成，在牛顿死后的1736年公开发表)中最早提出的。约瑟夫·拉弗森也曾于1690年在Analysis Aequationum中提出此方法。它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

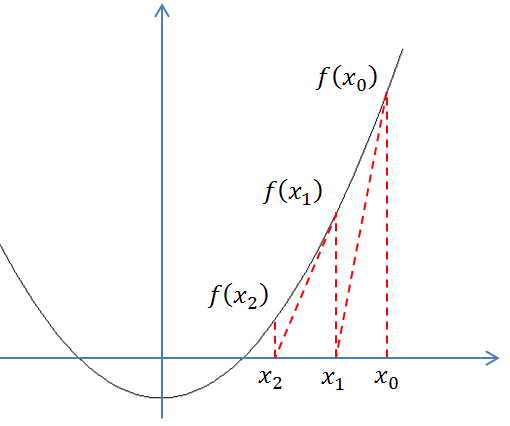
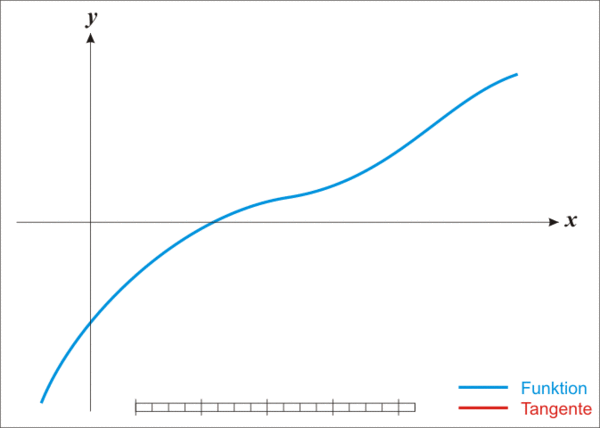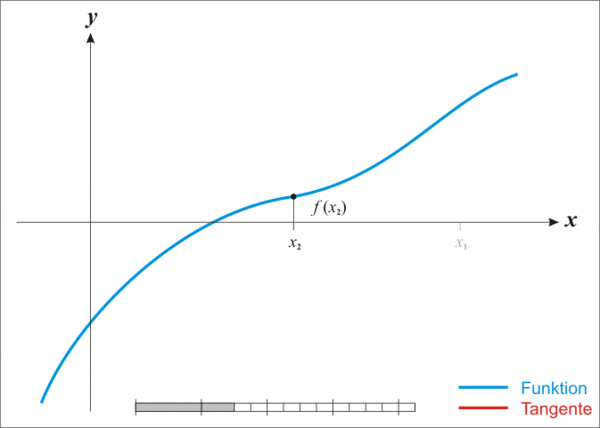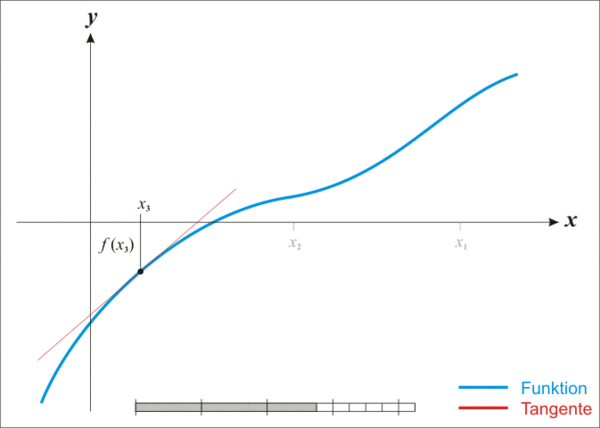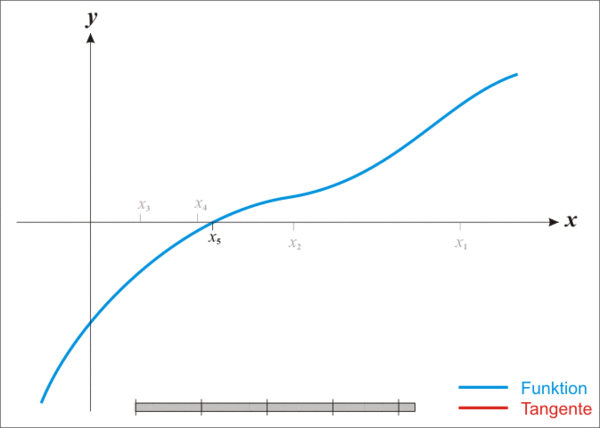
蓝线表示方程f(x)而红线表示切线. 可以看出\(x_{n+1}\)比\(x_n\)更靠近f所要求的根x.

既然牛顿迭代法可以用来求解方程的根，那么不妨以方程\(x^2=n\)为例，来试着求解它的根。为此。令\(f(x) = x^2 - n\)， 也就是相当于求解f(x)=0的解，如上图所示。 

       首先随便找一个初始值\(x_0\)，如果\(x_0\)不是解，做一个经过\((x_0,f( x_0))\)这个点的切线，与轴的交点为\(x_1\)。同理，如果\(x_1\)不是解，做一个经过\((x_1,f( x_1))\)这个点的切线，与轴的交点为\(x_2\)。 以此类推... 以这样的方式得到的会无限趋近于f(x)=0的解。 

判断\(x_i\)是否是f(x)=0的解有两种方法：1. 直接计算的值判断\(f(x_i)\)是否为0；2. 判断f(x)=0前后紧邻的两个解是否无限接近。 

经过这个点\((x_i, f(x_i))\)的切线方程为 \(f(x) = f(x_i) + f'(x_i)(x - x_i)\)

其中，\(f'(x_i)\)为\(f(x)\)的导数，本题中导数为\(2x\)。令切线方程等于0 (纵轴截距取0)，即可求出：

\(x_{i+1}=x_i - \frac{f(x_i)}{f'(x_i)}\)

代入\(f(x) = x^2 - n\)，继续化简：

\(x_{i+1}=x_i -\frac{x_i^2 - n}{2x_i} = x_i - \frac{x_i}{2} + \frac{n}{2x_i} = \frac{x_i}{2} + \frac{n}{2x_i}\)

基于上述迭代公式，可以给出了一个求平方根的算法。事实上，这也的确是很多语言中内置的开平方函数的实现方法。牛顿迭代法也同样适用于求解其他多次方程的解。

已AC代码：

#include <cstdio>
#include<climits>
#include<cmath>
using namespace std;
class Solution {
public:
int mySqrt(int x) {
    if(x < 0) return INT_MIN;
    if(x == 0) return 0;
    double pre = 0;  // res和pre是邻近的两次迭代结果，也可用变量adj表示邻近的值
    double res = 1;      // 在1附近开始找，迭代逼近目标值
    while(abs(res-pre) > 0.000001)  // 判断条件改为res-pre > 0.000001 || res-pre < -0.000001后，运行时间不变
    {
        pre = res;
        res = (res + x/res)/2.0;
    }
    return int(res);  // 返回值要求为int，需强制转换
}
};
// 下面为测试
int main()
{
    int x1=7;
    int x2=2222147483648;
    int x3=-5;
    Solution sol;
    int res1=sol.mySqrt(x1);
    int res2=sol.mySqrt(x2);
    int res3=sol.mySqrt(x3);
    printf("%d \n", res1);
    printf("%d \n", res2);
    printf("%d \n", res3);
    return 0;
}

P.S：本题是求解整数的平方根，并且返回值也是整型。在上述代码基础上稍微做修改，就可以同样适用于double(仅限方法1)。

#include <cstdio>
#include<climits>
#include<cmath>
using namespace std;
class Solution {
public:
double mySqrt(double x) {
    if(x < 0) return INT_MIN;
    if(x == 0) return 0;
    double pre = 0;
    double res = 1;        // 所求值为double时，迭代的初始值不能为0
 //   double res = 0.000001;
 //   double next = 1; //  res和pre是连续两次的迭代结果(邻近值)
    while(abs(res-pre) > 0.000001)  // 判断条件改为res-pre > 0.000001 || res-pre < -0.000001后，运行时间不变
    {
        pre = res;
        res = (res + x/res)/2.0;
    }
    return (res);
}
};
// 下面为测试
int main()
{
    double x1=7;
    double x2=2222147483648;
    double x3=-5;
    Solution sol;
    double res1=sol.mySqrt(x1);
    double res2=sol.mySqrt(x2);
    double res3=sol.mySqrt(x3);
    printf("%lf \n", res1);
    printf("%lf \n", res2);
    printf("%lf \n", res3);
    return 0;
}

PS: 由于所求值为double时，迭代的初始值不能为0。此代码中pre和res可以用res和next替换，见注释部分，当然循环中也得将pre换为next

解法2：二分搜索法

对于一个非负数n，它的平方根取整 \(\lfloor \sqrt(x) \rfloor \leq (\lfloor \frac{x}{2} \rfloor +1)\)，如下图所示，有x=1、2、4共3个整数交点，x>4以后\(\lfloor \sqrt(x) \rfloor \) 恒小于\(\lfloor \frac{x}{2} \rfloor +1\).

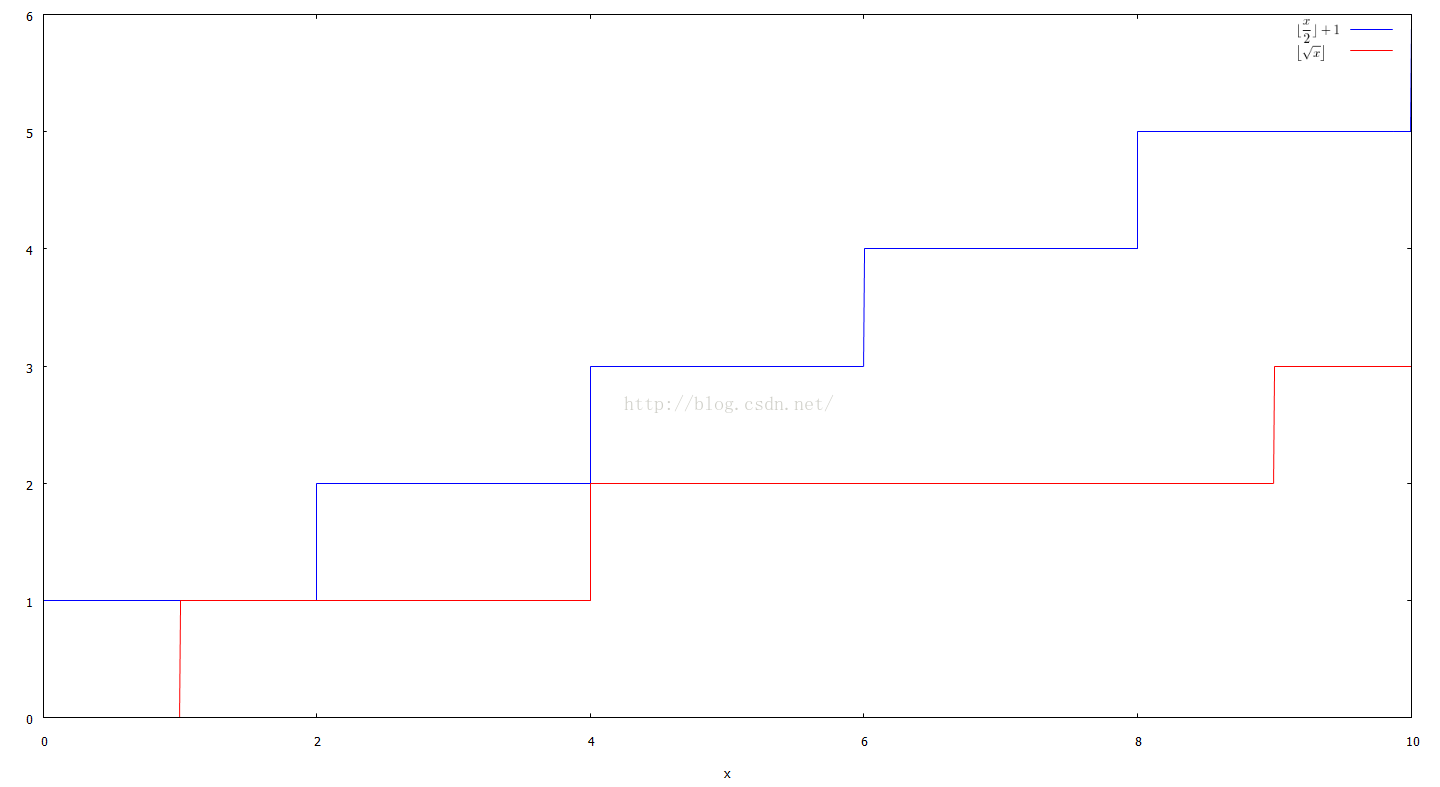
上图可在浏览器的新标签中打开，高清的

由于int sqrt(int x)接受的参数与返回值均为int型，故⌊√x⌋ ≤ (⌊x/2⌋+1)即等价于强数据类型语言(比如：C++、C、Java等)中的√x(目标值)≤ x/2+1 (x为自然数，非负整数). 于是在[0, x/2+1]这个范围内进行二分搜索，可以求出n的int型平方根，mid=(low+up)/2，其初值为x/2，结果应在[low, up]的mid或up处取得。如果用弱数据类型的语言(比如：PHP、Python、JavaScript等)实现此方法，需先自行ceiling或ceil进行下取整！

但此法不适用于double，因为此法利用了int型的特点。

AC代码：

#include <cstdio>
#include<climits>
using namespace std;
class Solution {
public:
    int mySqrt(int x) {
	if(x<0) return INT_MIN;
    long long low=0;
    long long up=x;
    while(low <= up)
	{
		long long mid=(low+up)/2; // 取中间值mid，在此处如果改为位运算居然使程序变慢了！
		long long square=mid*mid;
		if(x==square) return mid;  // 目标值等于mid处平方，提前退出循环出口
		else if(x>square) low=mid+1;  // 目标值大于mid处平方，在开区间(mid, up]中找，下界low的值调整为mid-1
			else up=mid-1;               // 目标值小于mid处平方，在开区间[low, mid)中找，上界up的值调整为mid+1
	}
	return up;
    }
};
// 下面为测试
int main()
{
    int x1=7;
    int x2=2222147483648;
	int x3=-5;
    Solution sol;
    int res1=sol.mySqrt(x1);
    int res2=sol.mySqrt(x2);
    int res3=sol.mySqrt(x3);
    printf("%d \n", res1);
    printf("%d \n", res2);
    printf("%d \n", res3);
    return 0;
}

此代码运行时间为8 ms，打败了39.64%的C++提交，除以2改成右移1位后，反而变慢了，12 ms，只打败了4.39%的C++提交...

相关链接：

http://www.cnblogs.com/AnnieKim/archive/2013/04/18/3028607.html (方法1代码测试未通过，方法2顺利)

http://blog.csdn.net/baimafujinji/article/details/50390841 (参考了循环的出口条件)