hdu-4678-sg

Mine

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 1731    Accepted Submission(s): 501

Problem Description

Have you ever played a game in Windows: Mine?
This game is played on a n*m board, just like the Pic(1)


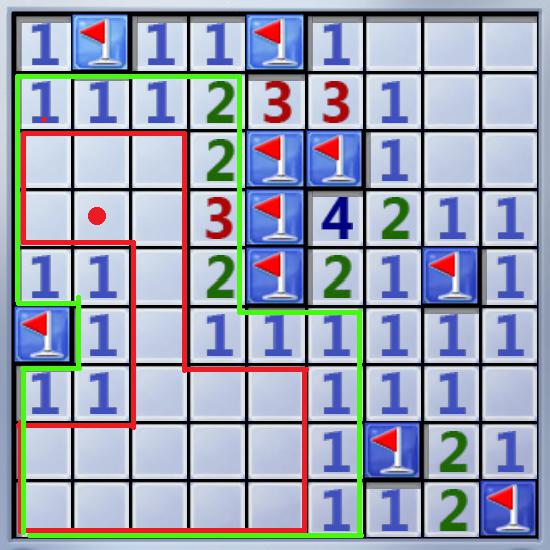
On the board, Under some grids there are mines (represent by a red flag). There are numbers ‘A(i,j)’ on some grids means there’re A(i,j) mines on the 8 grids which shares a corner or a line with gird(i,j). Some grids are blank means there’re no mines on the 8 grids which shares a corner or a line with them.
At the beginning, all grids are back upward.
In each turn, Player should choose a back upward grid to click.
If he clicks a mine, Game over.
If he clicks a grid with a number on it , the grid turns over.
If he clicks a blank grid, the grid turns over, then check grids in its 8 directions.If the new grid is a blank gird or a grid with a number,it will be clicked too.
So If we click the grid with a red point in Pic(1), grids in the area be encompassed with green line will turn over.
Now Xiemao and Fanglaoshi invent a new mode of playing Mine. They have found out coordinates of all grids with mine in a game. They also find that in a game there is no grid will turn over twice when click 2 different connected components.(In the Pic(2), grid at (1,1) will turn over twice when player clicks (0,0) and (2,2) , test data will not contain these cases).
Then, starting from Xiemao, they click the grid in turns. They both use the best strategy. Both of them will not click any grids with mine, and the one who have no grid to click is the loser.
Now give you the size of board N, M, number of mines K, and positions of every mine X_i,Y_i. Please output who will win.

 

Input

Multicase
The first line of the date is an integer T, which is the number of the text cases. (T<=50)
Then T cases follow, each case starts with 3 integers N, M, K indicates the size of the board and the number of mines.Then goes K lines, the ith line with 2 integer X_i,Y_i means the position of the ith mine.
1<=N,M<=1000 0<=K<=N*M 0<=X_i<N 0<=Y_i<M

 

Output

For each case, first you should print "Case #x: ", where x indicates the case number between 1 and T . Then output the winner of the game, either ”Xiemao” or “Fanglaoshi”. (without quotes)

 

Sample Input

2
3 3 0
3 3 1
1 1

 

Sample Output

Case #1: Xiemao
Case #2: Fanglaoshi

 

Source

2013 Multi-University Training Contest 8

 

　　　　给出一幅扫雷的地图，告诉你地雷所在位置，两个人轮流点击非炸弹且未显示出来的方格。点击的是空白格子的话会触发八联通格子的点击(如果他们未显示的话),点击的是数字格的话则只会显示点击的这一个格子，不再触发其他的操作。问先手是否处于胜态。

　　　可以将这个问题划分为一块块的小地图，所有联通的空白格和与他们相邻的数字格是一个独立的游戏，(除去他们之后单独的一个数字格也看作是一个独立的游戏),他们之间不会影响。只要计算出这些子问题的sg值就能推出胜态了。对于独立的一个数字格，sg=1。对于另一种情况，通过枚举可以发现，sg=(子地图中的数字格的数量)%2+1;

 

　　一开始dfs一直mle，换成了bfs就好了。还有注意地图是[0][0]开始的，，c。

　　

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <stdlib.h>
 #include <vector>
 #include <set>
 #include <queue>
 #include <stack>
 using namespace std;
 #define mp make_pair
 #define pii pair<int,int>
 int n,m,tot;
 int e[][];
 bool vis[][];
 int fx[][]={-,,,,,-,,,-,-,-,,,-,,};
 void bfs(int x,int y){
     queue<pair<int,int> >q;
     q.push(mp(x,y));
     while(!q.empty()){
         pii tmp=q.front();
         q.pop();
         if(vis[tmp.first][tmp.second]) continue;
         vis[tmp.first][tmp.second]=;
         if(e[tmp.first][tmp.second]==) {tot++;continue;}
         for(int i=;i<;++i){
             int dx=tmp.first+fx[i][];
             int dy=tmp.second+fx[i][];
             if(dx<||dy<||dx>n||dy>m||vis[dx][dy]) continue;
             q.push(mp(dx,dy));
         }
     }
 }
 int main(){
     int t,i,j,k,cas=;
     cin>>t;
     while(t--){
         memset(vis,,sizeof(vis));
         memset(e,,sizeof(e));
         cin>>n>>m>>k;
         int x,y;
         while(k--){
             scanf("%d%d",&x,&y);
             x++;
             y++;
             vis[x][y]=;
             e[x][y]=;
             for(i=;i<;++i){
                 int dx=x+fx[i][];
                 int dy=y+fx[i][];
                 if(dx>&&dy>&&dx<=n&&dy<=m&&vis[dx][dy]==) e[dx][dy]=;
             }
         }
         int sg=;
         for(i=;i<=n;++i){
             for(j=;j<=m;++j){
                 if(vis[i][j]||e[i][j]==) continue;
                     tot=;
                     bfs(i,j);
                     sg^=(tot%+);
             }
         }
         for(i=;i<=n;++i)
         for(j=;j<=m;++j)
         if(!vis[i][j]&&e[i][j]==) sg^=;
         printf("Case #%d: ",++cas);
         sg?puts("Xiemao"):puts("Fanglaoshi");
     }
     return ;
 }