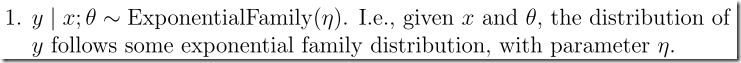【cs229-Lecture4】GLMS:选定指数分布族,如何用它来推导出GLM?
在Lecture4中有3部分内容:
- Newton’s method 牛顿方法
- Exceponential Family 指数分布族
- Generalized Linear Models 广义线性模型(GLMS)
牛顿法上一篇随便中已经讲过了,是平行于梯度下降算法的另一种最优化算法。
然后,视频中证明了伯努利分布和高斯分布都属是指数分布族中的特例的证明,实际上就是把这两种分布转化为指数分布族的形式,然后一一去对照,判断是否符合。
接下来,就讲到了当我们选定了一个指数分布族之后,如何用它来推导出一个广义线性模型(GLM),也就是本文想要讲述的内容。
首先,给出三个假设,同时我们以伯努利分布为例(01问题建模)来进行说明:
给定一个指数分布族,之前我们已经证明了伯努利分布是指数分布族的特例,因此,它满足第一个假设。
给定X,目标是求出以X为条件的T(y)的期望E[T(y)|x],即让学习算法输出h(x)=E[T(y)|x],在此处,这个期望值就等于因变量取1的概率,一般就写成P了。这个P涵盖了0-1因变量的信息,同时也能够用来比较直观地理解我们的问题:当自变量发生变化时,我们的目标变量取1的概率是怎样变化的。
假设因变量取1的概率跟自变量是线性关系。
之后会补充例子。
【cs229-Lecture4】GLMS:选定指数分布族,如何用它来推导出GLM?的更多相关文章
- 机器学习-牛顿方法&指数分布族&GLM
本节内容 牛顿方法 指数分布族 广义线性模型 之前学习了梯度下降方法,关于梯度下降(gradient descent),这里简单的回顾下[参考感知机学习部分提到的梯度下降(gradient desce ...
- Stanford大学机器学习公开课(四):牛顿法、指数分布族、广义线性模型
(一)牛顿法解最大似然估计 牛顿方法(Newton's Method)与梯度下降(Gradient Descent)方法的功能一样,都是对解空间进行搜索的方法.其基本思想如下: 对于一个函数f(x), ...
- [MCSM]Exponential family: 指数分布族
Exponential family(指数分布族)是一个经常出现的概念,但是对其定义并不是特别的清晰,今天好好看了看WIKI上的内容,有了一个大致的了解,先和大家分享下.本文基本是WIKI上部分内容的 ...
- Andrew Ng机器学习公开课笔记 -- Generalized Linear Models
网易公开课,第4课 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 前面介绍一个线性回归问题,符合高斯分布 一个分类问题,logstic回 ...
- [读书笔记] R语言实战 (十三) 广义线性模型
广义线性模型扩展了线性模型的框架,它包含了非正态的因变量分析 广义线性模型拟合形式: $$g(\mu_\lambda) = \beta_0 + \sum_{j=1}^m\beta_jX_j$$ $g( ...
- 斯坦福CS229机器学习课程笔记 part3:广义线性模型 Greneralized Linear Models (GLMs)
指数分布族 The exponential family 因为广义线性模型是围绕指数分布族的.大多数常用分布都属于指数分布族,服从指数分布族的条件是概率分布可以写成如下形式:η 被称作自然参数(nat ...
- CS229 笔记05
CS229 笔记05 生成学习方法 判别学习方法的主要思想是假设属于不同target的样本,服从不同的分布. 例如 \(P(x|y=0) \sim {\scr N}(\mu_1,\sigma_1^2) ...
- CS229 笔记04
CS229 笔记04 Logistic Regression Newton's Method 根据之前的讨论,在Logistic Regression中的一些符号有: \[ \begin{eqnarr ...
- CS229 Lecture 01
CS229 Lecture notes 01 机器学习课程主要分为4部分:监督学习:学习理论:无监督学习:增强学习. $x^{(i)}$表示特征,$y^{(i)}$表示目标,$i=1...m$.m是训 ...
随机推荐
- 将项目安装到Maven本地资源库
在Maven中,可以使用“mvn install”打包项目,并自动部署到本地资源库,让其他开发人员使用它. mvn install 注意,当“install”在执行阶段,上述所有阶段 “validat ...
- Can't read [proguard.ClassPathEntry@1a0c10f] (No such file or directory)
//该错误无法识别,是因为你使用了旧版本的proguard,建议你下载新版本4.5以上的proguard来替代Android SDK中使用的旧版sdcard 这样你就可以知道错误所在.因为只有4.5版 ...
- rrnDB数据库简介-16S基因多拷贝数的证据
16S基因作为mark gene在微生物群落结构的研究中发挥中重要作用, 但是候选的mark gene 肯定不止16S 一种,最新比较火热的功能基因,也可以作为mark gene.利用功能基因作为ma ...
- Linux中的软链接与硬链接
软链接相当于windows的快捷方式,当源文件不存在时,软链接失效. 链接是指向文件名,当指向的文件名字删除的时候,就找不到源文件了.硬链接是指向文件本身,删除一个文件名字,还是可以找到源文件的.ls ...
- shell脚本重启tomcat
1. 新建shell空脚本文件,如 /home/tr.sh,并设置权限 # chmod 750 /home/tr.sh 2. 设置文件形式: # sed -e 's/\^M//g' /home/tr. ...
- 关于SpringMVC的文件上传
关于文件的上传,之前写过2篇文章,基于Struts2框架,下面给出文章链接: <关于Struts2的文件上传>:http://www.cnblogs.com/lichenwei/p/392 ...
- 动态为页面添加CSS样式文件引用
动态为页面添加CSS样式文件引用: if (document.createStyleSheet) { //IE document.createStyleSheet("./Themes/Def ...
- 怎么安装ABBYY FineReader
ABBYY FineReader是市场领先的文字识别(OCR)软件,可快速方便地将扫描纸质文档.PDF文件和数码相机的图像转换成可编辑.可搜索信息,ABBYY FineReader 12是目前最新版本 ...
- Golang优秀开源项目汇总
https://blog.csdn.net/hackstoic/article/details/52008307
- Tomcat------如何查看80端口是否被占用
1.Window + R,打开“运行”窗口,输入cmd 2.输入netstat -nao,回车,一般来说80端口会被PID为4的程序占用 3.启动任务管理器,点击“查看”->“选择列” 4.勾选 ...