Fisher线性判别分析
Fisher线性判别分析
1、概述
在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口。
假设数据存在于d维空间中,在数学上,通过投影使数据映射到一条直线上,即维度从d维变为1维,这是容易实现的,但是即使数据在d维空间按集群形式紧凑分布,在某些1维空间上也会难以区分,为了使得数据在1维空间也变得容易区分,需要找到适当的直线方向,使数据映射在该直线上,各类样本集群交互较少。如何找到这条直线,或者说如何找到该直线方向,这是Fisher线性判别需要解决的问题。
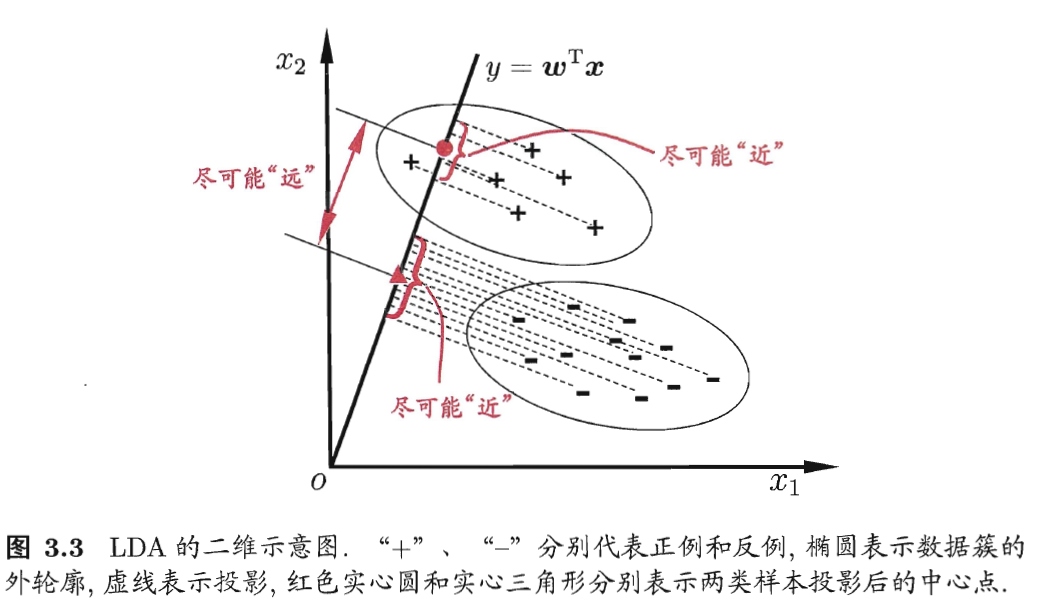
2、从d维空间变换到1维空间

3、介绍几个基本的参量
A. 在d维原始空间

B. 在1维映射空间

4、Fisher准则函数

5、学习算法推导




6、决策分类


Fisher线性判别分析的更多相关文章
- 线性判别分析(LDA)准则:FIsher准则、感知机准则、最小二乘(最小均方误差)准则
准则 采用一种分类形式后,就要采用准则来衡量分类的效果,最好的结果一般出现在准则函数的极值点上,因此将分类器的设计问题转化为求准则函数极值问题,即求准则函数的参数,如线性分类器中的权值向量. 分类器设 ...
- 线性判别分析(Linear Discriminant Analysis)转载
1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...
- 线性判别分析算法(LDA)
1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...
- (数据科学学习手札17)线性判别分析的原理简介&Python与R实现
之前数篇博客我们比较了几种具有代表性的聚类算法,但现实工作中,最多的问题是分类与定性预测,即通过基于已标注类型的数据的各显著特征值,通过大量样本训练出的模型,来对新出现的样本进行分类,这也是机器学习中 ...
- LDA(Linear discriminate analysis)线性判别分析
LDA 线性判别分析与Fisher算法完全不同 LDA是基于最小错误贝叶斯决策规则的. 在EMG肌电信号分析中,... 未完待续:.....
- 线性判别分析(LDA), 主成分分析(PCA)及其推导【转】
前言: 如果学习分类算法,最好从线性的入手,线性分类器最简单的就是LDA,它可以看做是简化版的SVM,如果想理解SVM这种分类器,那理解LDA就是很有必要的了. 谈到LDA,就不得不谈谈PCA,PCA ...
- 机器学习中的数学-线性判别分析(LDA), 主成分分析(PCA)
转:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html 版权声明: 本文由L ...
- 机器学习中的数学(4)-线性判别分析(LDA), 主成分分析(PCA)
版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...
- LDA 线性判别分析
LDA, Linear Discriminant Analysis,线性判别分析.注意与LDA(Latent Dirichlet Allocation,主题生成模型)的区别. 1.引入 上文介绍的PC ...
随机推荐
- 9/24matplotlib使用入门
---恢复内容开始--- matplotlib的使用中有好几种输出风格,有matlab风格,和官方文档的as风格,各有所长,本文对比介绍官方文档中的使用风格. 我们画图的目的是要将函数以图像显示出来, ...
- php 非递归实现分类树
本文实例讲述了php通过前序遍历树实现无需递归的无限极分类.分享给大家供大家参考.具体如下: 大家通常都是使用递归实现无限极分类都知道递归效率很低,下面介绍一种改进的前序遍历树算法,不适用递归实现无限 ...
- Hive四种数据导入方式介绍
问题导读 1.从本地文件系统中通过什么命令可导入数据到Hive表? 2.什么是动态分区插入? 3.该如何实现动态分区插入? 扩展: 这里可以和Hive中的三种不同的数据导出方式介绍进行对比? Hive ...
- php 获取随机数的几个方式
php 获取随机数的几个方式 1.直接获取从min-max的数,例如1-20:$randnum = mt_rand(1, 20); 2.在一个数组里面随机选择一个(验证码的时候需要字母.数字混合的情况 ...
- QImage与QPixmap完全解析
转载自http://www.civilnet.cn/bbs/browse.php?topicno=4691 用Qt程序在手机上显示一幅图片对编程人员来说是再基础不过的一件事情了.那么先让大家看两段代码 ...
- C/C++之内存分配
一.编译时与运行时的内存情况1.编译时不分配内存编译时是不分配内存的.此时只是根据声明时的类型进行占位,到以后程序执行时分配内存才会正确.所以声明是给编译器看的,聪明的编译器能根据声明帮你识别错误.2 ...
- ui-grid angularjs
<pre name="code" class="html"><!--ui-grid css--> <link rel=" ...
- SQL锁机制和事务隔离级别
摘自:http://www.cnblogs.com/haiyang1985/archive/2009/02/27/1399641.html 锁机制 NOLOCK和READPAST的区别. 1. ...
- Linux系统的vi命令
Linux系统的vi命令 vi编辑命令 1,格式: #vi filename 2,用法: //打开或新建文件,并将光标置于第一行首 #vi + filename //打开文件,并将光标置于第n行首 # ...
- poj 2369 Permutations - 数论
We remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Les ...
