c++作业题sin公式

今日 有一位同样读大一的朋友向我求助有关c++的作业题 他说他的程序逻辑正确 但是结果的精度不对

题目如下:

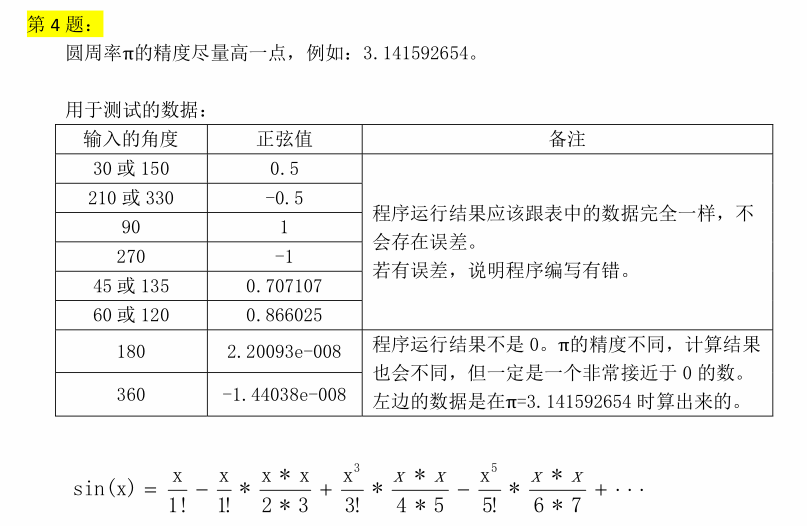
这是一道看起来十分简单的作业题 我按照要求快速地写了一个版本 不出所料 一样遇到了精度问题

为什么会出现这种问题?

首先 计算机中的浮点数是不够精确的 这是为了运算速度所做的牺牲

在我写的代码中 使用的是double 为了使结果精确 要能尽量减少不必要的计算过程

而我用了cmath头文件中的pow函数 这使得double会被计算很多次导致结果精度降低

于是我决定写一个无pow版本 从公式出发 思路如下:

原式化简:

sin(x) = x/1! - x^3/(1!*2*3) + x^5/(3!*4*5) - x^7/(5!*6*7) ...

拆分:

sin(x)= x/1!
	- x^3/(1!*2*3)
	+ x^5/(3!*4*5)
	- x^7/(5!*6*7)
	...

拆分之后我们可以尝试用一个变量去替换其中的数字:

sin(x)= x/1!
[i=1] - x^3/(i!*(i+1)*(i+2))
[i=3] + x^5/(i!*(i+1)*(i+2))
[i=5] - x^7/(i!*(i+1)*(i+2))
[i=n] ...

引入一个变量p 替换幂:

p=x
sin(x)= p/1!
[i=1,p=p*x*x] - p/(i!*(i+1)*(i+2))
[i=3,p=p*x*x] + p/(i!*(i+1)*(i+2))
[i=5,p=p*x*x] - p/(i!*(i+1)*(i+2))
[i=n,p=p*x*x] ...

再引入一个变量f 替换阶乘:

f=1
p=x
sin(x)= p/f
[i=1,p=p*x*x,f=f*(i+1)*(i+2)] - p/f
[i=3,p=p*x*x,f=f*(i+1)*(i+2)] + p/f
[i=5,p=p*x*x,f=f*(i+1)*(i+2)] - p/f
[i=n,p=p*x*x,f=f*(i+1)*(i+2)] ...

再引入一个变量n 替换其中的负号:

n=1
f=1
p=x
sin(x)= p/f
[i=1,p=p*x*x,f=f*(i+1)*(i+2),n=-n] + n*p/f
[i=3,p=p*x*x,f=f*(i+1)*(i+2),n=-n] + n*p/f
[i=5,p=p*x*x,f=f*(i+1)*(i+2),n=-n] + n*p/f
[i=n,p=p*x*x,f=f*(i+1)*(i+2),n=-n] ...

现在每项的式子完全相同了 只需将其转换成对应的程序
我们要考虑结束条件 即当其中一项的绝对值小于1.0e-7时 结束这个循环

最终答案 :

 double x;
 cout << "请输入角度值:";
 cin >> x;

 x = x * 3.141592654 / ;

 double n = ;
 double f = ;
 double p = x;
 double i = -;

 double term = ;
 double result = p / f;

 while ()
 {
     i += ;
     p = p * x * x;
     f = f * (i + ) * (i + );
     n = -n;
     term = p / f;
     if (term < 1.0e-7)
         break;
     result = result + n * term;
 }
 cout << "对应的sin值为:" << result << endl;

结果正确:

再看看朋友的代码:

 double angel,term,sum=,i=,multi=,sign=-;
 const double pi=3.141592654;
 cout<<"请输入角度值:";
 cin>>angel;
 angel=angel*pi/;
 term=angel;
 while(term>=1.0e-7||term<=-1.0e-7)
 {
     sum+=term;
     angel*=angel*angel;
     multi*=(i+)*(i+);
     term=sign*angel/multi;
     sign*=-;
     i+=;
 }
 cout<<"对应的sin值为:"<<sum<<endl;

结果:

思路大致和我相同 但是其中一步 angel*=angel*angel; 不对
在我的代码中 这一步对应的是 p = p * x * x; 其中x是不变的 他代码的这一部分并不等效于sin公式

END