懒癌晚期学图论的时候自己用C语言写了个求可达性矩阵的算法~

可达性矩阵算法~

直接上代码

#include <iostream>
#include <cstring>
using namespace std;
#define n 5
void print(int a[n][n]);
void print1(int a[n][n]);
void multiply(int a[n][n],int b[n][n],int c[n][n]);
void add(int a[n][n],int b[n][n]);
int main(){
    int a[n][n],b[n][n],c[n][n],d[n][n];
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            cin>>a[i][j];
            b[i][j] = a[i][j];
            d[i][j] = a[i][j];

        }
    }cout<<"A:"<<endl;
    print(a);
    for(int i = 0;i<n-1;i++){
        cout<<"A"<<i+2<<":"<<endl;
        if(i%2){
            memset(a,0,sizeof(a));
            multiply(c,b,a);
            add(d,a);
            print(a);

        }else{
            memset(c,false,sizeof(c));
            multiply(a,b,c);
            add(d,c);
            print(c);
        }
    }
    cout<<"R:"<<endl;
    print(d);
    cout<<"P:"<<endl;
    print1(d);
}
void multiply(int a[n][n],int b[n][n],int c[n][n]){
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            for(int k = 0;k<n;++k){
                c[i][j] = c[i][j]+(a[i][k]*b[k][j]);

            }
        }
    }
}void print(int a[n][n]){
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            cout<<a[i][j]<<(j<n-1?" ":"");

        }cout<<endl;

    }
}
void add(int a[n][n],int b[n][n]){
    for(int i=0;i<n;++i){
        for(int j=0;j<n;++j){
            a[i][j]=a[i][j]+b[i][j];
        }
    }
}void print1(int a[n][n]){
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            cout<<(a[i][j]?1:0)<<(j<n-1?" ":"");

        }cout<<endl;

    }
}

结果图

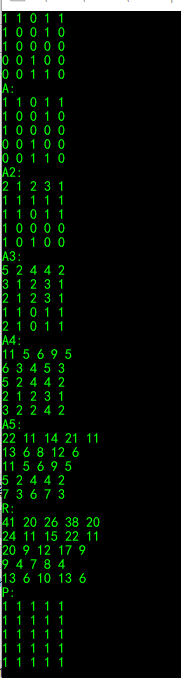
布尔型

#include <iostream>
#include <cstring>
using namespace std;
#define n 5
void print(bool a[n][n]);
void multiply(bool a[n][n],bool b[n][n],bool c[n][n]);
void add(bool a[n][n],bool b[n][n]);
int main(){
    bool a[n][n],b[n][n],c[n][n],d[n][n];
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            cin>>a[i][j];
            b[i][j] = a[i][j];
            d[i][j] = a[i][j];

        }
    }cout<<"A:"<<endl;
    print(a);
    for(int i = 0;i<n-1;i++){
        cout<<"A"<<i+2<<":"<<endl;
        if(i%2){
            memset(a,false,sizeof(a));
            multiply(c,b,a);
            add(d,a);
            print(a);

        }else{
            memset(c,false,sizeof(c));
            multiply(a,b,c);
            add(d,c);
            print(c);
        }
    }
    cout<<"P:"<<endl;
    print(d);
}
void multiply(bool a[n][n],bool b[n][n],bool c[n][n]){
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            for(int k = 0;k<n;++k){
                c[i][j] = c[i][j]||(a[i][k]&&b[k][j]);

            }
        }
    }
}void print(bool a[n][n]){
    for(int i = 0;i<n;++i){
        for(int j = 0;j<n;++j){
            cout<<a[i][j]<<(j<n-1?" ":"");

        }cout<<endl;

    }
}
void add(bool a[n][n],bool b[n][n]){
    for(int i=0;i<n;++i){
        for(int j=0;j<n;++j){
            a[i][j]=a[i][j]||b[i][j];
        }
    }
}

其实就是把乘和加的地方改一改就好了！