SDOI2015约数个数和

题目描述

题解：

有一个式子：

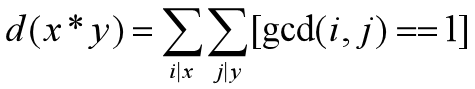
证明先不说了。

然后倒一波反演：

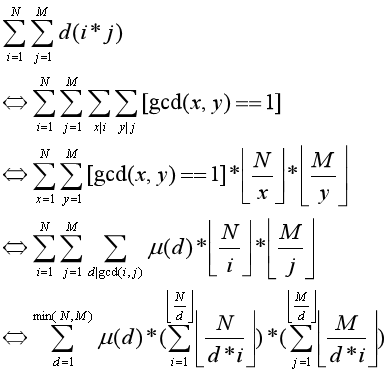
然后整除分块就好了。

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 50050
#define ll long long
int t,n,m;
int pri[N],cnt,mu[N];
ll sum[N],f[N];
bool vis[N];
void get_mu()
{
    mu[]=sum[]=;
    for(int i=;i<=;i++)
    {
        if(!vis[i])
        {
            pri[++cnt]=i;
            mu[i]=-;
        }
        for(int j=;j<=cnt&&i*pri[j]<=;j++)
        {
            vis[i*pri[j]]=;
            if(i%pri[j])mu[i*pri[j]]=-mu[i];
            else break;
        }
        sum[i]=sum[i-]+mu[i];
    }
}
void get_f()
{
    for(int x=;x<=;x++)
    for(int i=,nxt;i<=x;i=nxt+)
    {
        nxt=x/(x/i);
        f[x]+=1ll*(nxt-i+)*(x/i);
    }
}
int main()
{
    scanf("%d",&t);
    get_mu();
    get_f();
    while(t--)
    {
        scanf("%d%d",&n,&m);
        if(n>m)swap(n,m);
        ll ans = ;
        for(int i=,nxt;i<=n;i=nxt+)
        {
            nxt = min(n/(n/i),m/(m/i));
            ans+=1ll*(sum[nxt]-sum[i-])*f[n/i]*f[m/i];
        }
        printf("%lld\n",ans);
    }
    return ;
}