HDU3338 Kakuro Extension —— 最大流、方格填数类似数独
题目链接：https://vjudge.net/problem/HDU-3338
Kakuro Extension
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2419 Accepted Submission(s): 840
Special Judge
Kakuro puzzle is played on a grid of "black" and "white" cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form "runs" and some amount of black cells. "Run" is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one "run". Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal "run" always has a number in the black half-cell to its immediate left, and each vertical "run" always has a number in the black half-cell immediately above it. These numbers are located in "black" cells and are called "clues".The rules of the puzzle are simple:
1.place a single digit from 1 to 9 in each "white" cell
2.for all runs, the sum of all digits in a "run" must match the clue associated with the "run"
Given the grid, your task is to find a solution for the puzzle.
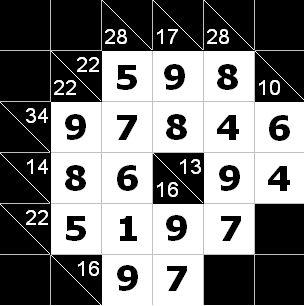
Picture of the first sample input Picture of the first sample output
.......— "white" cell;
XXXXXXX— "black" cell with no clues;
AAA\BBB— "black" cell with one or two clues. AAA is either a 3-digit clue for the corresponding vertical run, or XXX if there is no associated vertical run. BBB is either a 3-digit clue for the corresponding horizontal run, or XXX if there is no associated horizontal run.
The first row and the first column of the grid will never have any white cells. The given grid will have at least one "white" cell.It is guaranteed that the given puzzle has at least one solution.
XXXXXXX XXXXXXX 028\XXX 017\XXX 028\XXX XXXXXXX
XXXXXXX 022\022 ....... ....... ....... 010\XXX
XXX\034 ....... ....... ....... ....... .......
XXX\014 ....... ....... 016\013 ....... .......
XXX\022 ....... ....... ....... ....... XXXXXXX
XXXXXXX XXX\016 ....... ....... XXXXXXX XXXXXXX
5 8
XXXXXXX 001\XXX 020\XXX 027\XXX 021\XXX 028\XXX 014\XXX 024\XXX
XXX\035 ....... ....... ....... ....... ....... ....... .......
XXXXXXX 007\034 ....... ....... ....... ....... ....... .......
XXX\043 ....... ....... ....... ....... ....... ....... .......
XXX\030 ....... ....... ....... ....... ....... ....... XXXXXXX
_ _ 5 8 9 _
_ 7 6 9 8 4
_ 6 8 _ 7 6
_ 9 2 7 4 _
_ _ 7 9 _ _
_ _ _ _ _ _ _ _
_ 1 9 9 1 1 8 6
_ _ 1 7 7 9 1 9
_ 1 3 9 9 9 3 9
_ 6 7 2 4 9 2 _
题意：
给定一个n*m的矩阵，为其中的白格填上范围为1~9的数，并且满足横之和、纵之和的限制，限制记录在黑格子上。类似于数独游戏，要求输出一组可行解。
题解：
可知横之和的和必定等于纵之和的和，因为横之和的和是所有白格子的和， so does 纵之和的和。因此，我们可以用网络流来解题，建图如下：
1.先对行进行分块，然后再对列进行分块，因为同一行或同一列不一定属于同一个run。
2.建立超级源点，超级源点连向每一个横之和结点，容量为横之和。
3.对于每个白格，将其横坐标所属的横之和结点连向其纵坐标所属的纵之和结点，容量下界为1，容量上界为9。
4.建立超级汇点，每个纵之和结点连向超级汇点，容量为纵之和。
5.回顾上述建图方法，发现白格建的边容量下界（一般情况都是没有下界的，即为0），不好处理。但是可以知道容量下界都为1，那么，我们可以先为每个白格子都分一个1，表明这个1是必须的，毋庸置疑。因此，就可以去掉白格子所建的边的容量下界了，而容量上界也因此改为8.
6.由于“横之和的和=纵之和的和”，“横之和的和”的流量由超级源点发出，“纵之和的和”的流量由超级汇点接收，且可知如果有解，那么白格子的存在（调节）必定能使每条：超级汇点-->“横之和”结点 的边满流，而满流时必定是最大流。因此我们可以跑最大流算法，然后再提取每条白格子所建边的流量信息，即可知道每个白格子应该填上什么数。
写法一：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int mod = 1e9+;
const int MAXM = 1e5+;
const int MAXN = 1e4+; struct Edge
{
int to, next, cap, flow;
}edge[MAXM];
int tot, head[MAXN];
int gap[MAXN], dep[MAXN], pre[MAXN], cur[MAXN]; void init()
{
tot = ;
memset(head, -, sizeof(head));
} void add(int u, int v, int w)
{
edge[tot].to = v; edge[tot].cap = w; edge[tot].flow = ;
edge[tot].next = head[u]; head[u] = tot++;
edge[tot].to = u; edge[tot].cap = ; edge[tot].flow = ;
edge[tot].next = head[v]; head[v] = tot++;
} int sap(int start, int end, int nodenum)
{
memset(dep, , sizeof(dep));
memset(gap, , sizeof(gap));
memcpy(cur, head, sizeof(head));
int u = pre[start] = start, maxflow = ,aug = INF;
gap[] = nodenum;
while(dep[start]<nodenum)
{
loop:
for(int i = cur[u]; i!=-; i = edge[i].next)
{
int v = edge[i].to;
if(edge[i].cap-edge[i].flow && dep[u]==dep[v]+)
{
aug = min(aug, edge[i].cap-edge[i].flow);
pre[v] = u;
cur[u] = i;
u = v;
if(v==end)
{
maxflow += aug;
for(u = pre[u]; v!=start; v = u,u = pre[u])
{
edge[cur[u]].flow += aug;
edge[cur[u]^].flow -= aug;
}
aug = INF;
}
goto loop;
}
}
int mindis = nodenum;
for(int i = head[u]; i!=-; i = edge[i].next)
{
int v=edge[i].to;
if(edge[i].cap-edge[i].flow && mindis>dep[v])
{
cur[u] = i;
mindis = dep[v];
}
}
if((--gap[dep[u]])==)break;
gap[dep[u]=mindis+]++;
u = pre[u];
}
return maxflow;
} char str[];
int Map[][], run[][][]; //用于记录原始图案
int xid[][], yid[][];
int xrun[], yrun[], index[][];
int main()
{
int n, m;
while(scanf("%d%d", &n,&m)!=EOF)
{
for(int i = ; i<=n; i++)
for(int j = ; j<=m; j++)
{
scanf("%s", str);
if(str[]=='.') Map[i][j] = ;
else
{
Map[i][j] = ;
if(str[]!='X') run[i][j][] = (str[]-'')*+(str[]-'')*+(str[]-'');
if(str[]!='X') run[i][j][] = (str[]-'')*+(str[]-'')*+(str[]-'');
}
} int xcnt = , ycnt = ;
for(int i = ; i<=n; i++)
for(int j = ; j<=m; j++)
{
if(Map[i][j])
{
if(!Map[i][j-]) //横流
{
xid[i][j] = xcnt;
xrun[xcnt++] = run[i][j-][];
}else xid[i][j] = xid[i][j-];
xrun[xid[i][j]]--; if(!Map[i-][j]) //纵流
{
yid[i][j] = ycnt;
yrun[ycnt++] = run[i-][j][];
}else yid[i][j] = yid[i-][j];
yrun[yid[i][j]]--;
}
} int start = xcnt+ycnt, end = xcnt+ycnt+;
init();
for(int i = ; i<=n; i++)
for(int j = ; j<=m; j++)
{
if(Map[i][j])
{
add(xid[i][j], xcnt+yid[i][j], );
index[i][j] = tot-; //记录这个空格所对应的边
}
}
for(int i = ; i<xcnt; i++) add(start, i, xrun[i]);
for(int i = ; i<ycnt; i++) add(xcnt+i, end, yrun[i]); sap(start, end, xcnt+ycnt+);
for(int i = ; i<=n; i++)
{
for(int j = ; j<=m; j++)
{
printf("%c", Map[i][j]?(edge[index[i][j]].flow+''):'_');
if(j<m) printf(" ");
}
printf("\n");
}
}
}
写法二：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int mod = 1e9+;
const int MAXM = 1e5+;
const int MAXN = 1e4+; struct Edge
{
int to, next, cap, flow;
}edge[MAXM];
int tot, head[MAXN];
int gap[MAXN], dep[MAXN], pre[MAXN], cur[MAXN]; void init()
{
tot = ;
memset(head, -, sizeof(head));
} void add(int u, int v, int w)
{
edge[tot].to = v; edge[tot].cap = w; edge[tot].flow = ;
edge[tot].next = head[u]; head[u] = tot++;
edge[tot].to = u; edge[tot].cap = ; edge[tot].flow = ;
edge[tot].next = head[v]; head[v] = tot++;
} int sap(int start, int end, int nodenum)
{
memset(dep, , sizeof(dep));
memset(gap, , sizeof(gap));
memcpy(cur, head, sizeof(head));
int u = pre[start] = start, maxflow = ,aug = INF;
gap[] = nodenum;
while(dep[start]<nodenum)
{
loop:
for(int i = cur[u]; i!=-; i = edge[i].next)
{
int v = edge[i].to;
if(edge[i].cap-edge[i].flow && dep[u]==dep[v]+)
{
aug = min(aug, edge[i].cap-edge[i].flow);
pre[v] = u;
cur[u] = i;
u = v;
if(v==end)
{
maxflow += aug;
for(u = pre[u]; v!=start; v = u,u = pre[u])
{
edge[cur[u]].flow += aug;
edge[cur[u]^].flow -= aug;
}
aug = INF;
}
goto loop;
}
}
int mindis = nodenum;
for(int i = head[u]; i!=-; i = edge[i].next)
{
int v=edge[i].to;
if(edge[i].cap-edge[i].flow && mindis>dep[v])
{
cur[u] = i;
mindis = dep[v];
}
}
if((--gap[dep[u]])==)break;
gap[dep[u]=mindis+]++;
u = pre[u];
}
return maxflow;
} char str[];
int Map[][], run[][][];
int xid[][], yid[][];
int xbelong[], ybelong[], xrun[], yrun[];
int result[][];
int main()
{
int n, m;
while(scanf("%d%d", &n,&m)!=EOF)
{
for(int i = ; i<=n; i++)
for(int j = ; j<=m; j++)
{
scanf("%s", str);
if(str[]=='.') Map[i][j] = ;
else
{
Map[i][j] = ;
if(str[]!='X') run[i][j][] = (str[]-'')*+(str[]-'')*+(str[]-'');
if(str[]!='X') run[i][j][] = (str[]-'')*+(str[]-'')*+(str[]-'');
}
} int xcnt = , ycnt = ;
for(int i = ; i<=n; i++)
for(int j = ; j<=m; j++)
{
if(Map[i][j])
{
if(!Map[i][j-])
{
xid[i][j] = xcnt;
xrun[xcnt] = run[i][j-][];
xbelong[xcnt++] = i;
}else xid[i][j] = xid[i][j-];
xrun[xid[i][j]]--; if(!Map[i-][j])
{
yid[i][j] = ycnt;
yrun[ycnt] = run[i-][j][];
ybelong[ycnt++] = j;
}else yid[i][j] = yid[i-][j];
yrun[yid[i][j]]--;
}
} int start = xcnt+ycnt, end = xcnt+ycnt+;
init();
for(int i = ; i<=n; i++)
for(int j = ; j<=m; j++)
{
if(Map[i][j])
add(xid[i][j], xcnt+yid[i][j], );
}
for(int i = ; i<xcnt; i++) add(start, i, xrun[i]);
for(int i = ; i<ycnt; i++) add(xcnt+i, end, yrun[i]); sap(start, end, xcnt+ycnt+);
memset(result, , sizeof(result)); for(int u = ; u<xcnt; u++)
for(int i = head[u]; i!=-; i=edge[i].next)
{
int v = edge[i].to-xcnt;
if(v>=ycnt) continue;
int x = xbelong[u], y = ybelong[v];
if(Map[x][y]) result[x][y] = edge[i].flow+;
} for(int i = ; i<=n; i++)
{
for(int j = ; j<=m; j++)
{
if(Map[i][j]) printf("%d", result[i][j]);
else printf("_");
if(j<m) printf(" ");
}
printf("\n");
}
}
}
HDU3338 Kakuro Extension —— 最大流、方格填数类似数独的更多相关文章
- HDU3338 Kakuro Extension(最大流+思维构图)
这道题一定要写一下,卡了好久. 题意: 有黑白两种方格,最上边一行和最左边一列一定是黑色,然后其余的地方有可能是黑色,有可能是白色,和白色相邻的黑色方格里有数字(1个或2个), 现在要求在白色方格里填 ...
- hdu3338 Kakuro Extension 最大流
If you solved problem like this, forget it.Because you need to use a completely different algorithm ...
- java算法 蓝桥杯（题+答案） 方格填数
6.方格填数 (结果填空) 如下的10个格子 (如果显示有问题,也可以参看[图1.jpg]) 填入0~9的数字.要求:连续的两个数字不能相邻.(左右.上下.对角都算相邻) 一共有多少种可能的填数方案 ...
- 蓝桥杯比赛javaB组练习《方格填数》
方格填数 如下的10个格子 +--+--+--+ | | | |+--+--+--+--+| | | | |+--+--+--+--+| | | |+--+--+--+ ( ...
- java算法 第七届 蓝桥杯B组（题+答案） 6.方格填数
6.方格填数 (结果填空) 如下的10个格子 (如果显示有问题,也可以参看[图1.jpg]) 填入0~9的数字.要求:连续的两个数字不能相邻.(左右.上下.对角都算相邻) 一共有多少种可能的填数方案 ...
- c++_方格填数（最新方法）
方格填数 如下的10个格子 +--+--+--+ | | | |+--+--+--+--+| | | | |+--+--+--+--+| | | |+--+--+--+ (如果显示有问题,也可以参 ...
- 第七届蓝桥杯试题c/c++A组方格填数 回溯法
方格填数如下的10个格子 +--+--+--+ | | | |+--+--+--+--+| | | | |+--+--+--+--+| | | |+--+--+--+(如果 ...
- 第七届蓝桥杯javaB组真题解析-方格填数（第六题）
题目 /* 方格填数 如下的10个格子 +--+--+--+ | | | | +--+--+--+--+ | | | | | +--+--+--+--+ | | | | +--+--+--+ (如果显 ...
- DFS(深度优先搜索遍历求合格条件总数)--07--DFS--蓝桥杯方格填数
此题方法多种,我用规范的DFS来求解 题目:方格填数 如下的10个格子,填入0~9的数字.要求:连续的两个数字不能相邻. (左右.上下.对角都算相邻)一共有多少种可能的填数方案? 输出 请填写表示 ...
随机推荐
- 记一次Jenkins 打包异常 ERROR: Exception when publishing, exception message [Failure]
今天早上打包一直都没有问题,突然有一次打包突然出现异常现象,如下: ERROR: Exception when publishing, exception message [Failure] Buil ...
- angularjs bootstrap 简介
1.angular特色 数据双向绑定 模块化 var myapp=angular.module... 控制器 myapp.controller(){} 2.bootstrap特色 栅格结构 cs ...
- DOM对象之查找标签&属性操作
HTML DOM (文档对象模型) DOM(Document Object Model)是一套对文档的内容进行抽象和概念化的方法. JavaScript对DOM进行了实现,对应于JavaScript中 ...
- AC日记——最大子段和 洛谷 P1115
题目描述 给出一段序列,选出其中连续且非空的一段使得这段和最大. 输入输出格式 输入格式: 输入文件maxsum1.in的第一行是一个正整数N,表示了序列的长度. 第2行包含N个绝对值不大于10000 ...
- B站papi酱、陈一发、李云龙
李云龙-花田错 https://www.bilibili.com/video/av10842071/?from=timeline&isappinstalled=1 李云龙:你猜旅长怎么说? h ...
- Spring中Beans的自动装配概述
以下内容引用自http://wiki.jikexueyuan.com/project/spring/beans-autowiring.html: 在之前的做法上会参照这样的顺序:1.使用<bea ...
- 【RESTful】1.理解REST和RESTful
简记:一套设计良好的RESTful可以帮助互联网产品支持[单个服务端+多个客户端]的场景!!!
- 更改Tomcat命令行窗体标题
在windows下启动多个tomcat时.不好区分哪个tomcat相应哪个服务,能够通过下面方法设置Tomcat命令行窗体的标题: 1.在%tomcat_home%\bin\catalina.b ...
- AWS向中国有限预览客户推出多级别AWS支持服务
2014年9月26日 在AWS中国(北京)区域有限预览服务开展的过程中.很多客户都提出了对AWS支持服务(AWS Support)的需求. AWS客户在向云端部署系统,日常运营维护以及关键性项目实 ...
- Android开发系列（二十一）：Spinner的功能和使用方法以及实现列表选择框
Spinner是一个列表选择框.相当于弹出一个菜单供用户进行选择. Spinner继承AdapterView Spinnet支持的XML的属性: android:entries:使用数组资源设置该下拉 ...